Rumus Menghitung Unsur-Unsur Lingkaran & Contoh | Matematika Kelas 8

Ada apa aja sih unsur-unsur lingkaran itu? Bagaimana cara menghitungnya? Yuk simak cara menghitung unsur-unsur lingkaran dalam artikel Matematika kelas 8 ini!

—

Hai haiii! Kalian masih ingat kan apa saja unsur-unsur lingkaran? Unsur lingkaran itu bukan meliputi angin, air, api, dan udara yang dikuasai Avatar the Legend of Aang, ya, hehehe.

Coba sebutkan apa saja unsur lingkaran!

(kalo kamu masih inget, cus ke kolom komentar bawah dong :P)

Unsur lingkaran itu terdiri dari titik pusat, jari-jari (r), diameter (d), tali busur, busur, juring, tembereng, dan apotema. Masih inget kan?

Kalau kamu masih lupa-lupa ingat, coba perhatikan gambar di bawah ini ya!

Unsur-Unsur Lingkaran

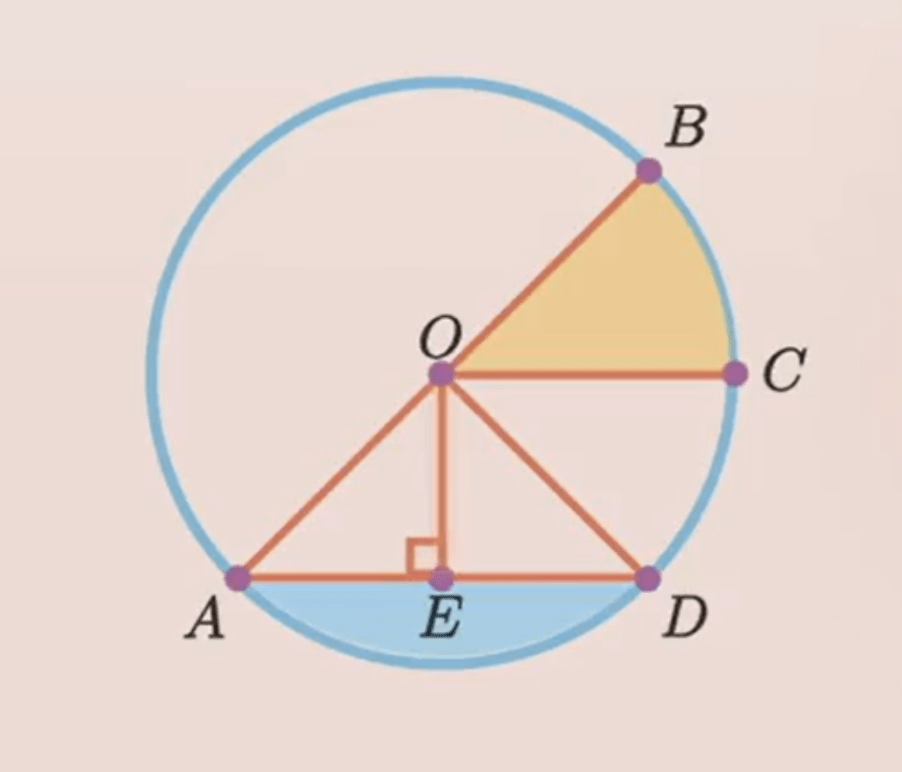
(sumber: Video Belajar Ruangguru)

• Titik Pusat (titik O)
• Jari-jari (ruas garis OA, OB, OC, OD).
• Diameter (ruas garis AB)
• Tali Busur (ruas garis AD dan AB)
• Busur (garis lengkung AD, DC, AB)
• Juring (daerah BOC)
• Tembereng (daerah warna biru)
• Apotema (ruas garis OE)

Nah, kalau kamu udah inget tentang masing-masing perbedaan unsur-unsur lingkaran tersebut,  sekarang kita akan lanjut mencari tahu tentang cara menghitung unsur-unsur lingkaran. Simak baik-baik ya!

Baca Juga: Rumus Luas dan Volume Kubus serta Contoh Soal

1. Rumus Keliling dan Luas Lingkaran

Apa bedanya keliling lingkaran dan luas lingkaran? Keliling lingkaran adalah panjang garis lengkung dari suatu lingkaran, sedangkan luas lingkaran merupakan luas daerah yang dibatasi oleh busur lingkaran atau keliling lingkaran.

Berikut rumus untuk menghitung keliling dan luas lingkaran.

Contoh Soal!

1. Diketahui lingkaran dengan jari-jari 20 cm, keliling lingkaran tersebut adalah …

Pembahasan:

Diketahui: r = 20 cm

Ditanya: Keliling lingkaran (K) …?

Jawab:

K = 2 × π × r
K = 2 × 3,14 × 20
K = 125,6 cm

Jadi, keliling lingkaran tersebut adalah 125,6 cm.

2. Jika diketahui sebuah lingkaran mempunyai diameter 10 cm. Berapakah luas lingkaran tersebut?

Pembahasan:

Diketahui: d = 10 cm

Ditanya: Luas lingkaran (L) …?

Jawab:

L = 1/4 × π × d²
L = (1/4) × 3,14 × (10)²
L = (1/4) × 314
L = 78,5 cm²

Jadi, luas lingkaran tersebut adalah 78,5 cm².

2. Rumus Menghitung Sudut Pusat dan Sudut Keliling

Ngejar Si Mamat makin bikin pusing (Tjakeeeep~~~)

Yuk, belajar sudut pusat dan sudut keliling.

Sama-sama sudut yang ada di lingkaran tapi mereka berdua beda. Kadang kalau ga paham konsep, bisa bingung bedain keduanya. Tapi santuy, bareng Ruangguru, kamu jadi bisa ngebedain antara sudut pusat dan sudut keliling. Perhatiin deh pengertiannya sama gambarnya.

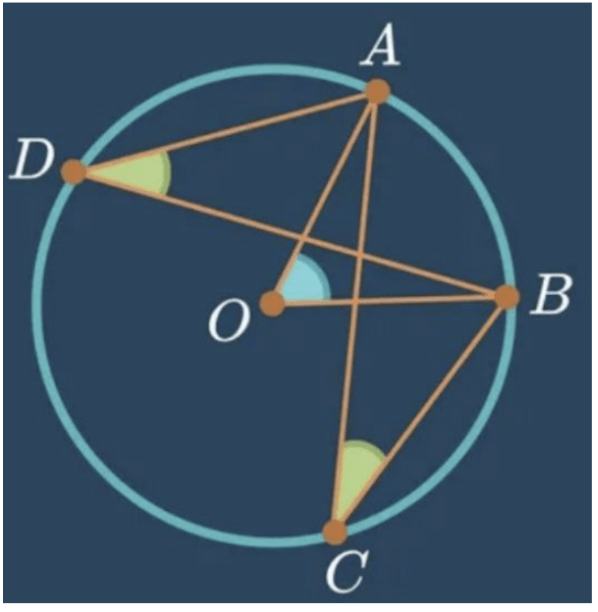
(sumber: Video Belajar Ruangguru)

Sudut pusat itu merupakan daerah sudut yang dibatasi oleh dua jari-jari lingkaran yang titik sudutnya merupakan titik pusat lingkaran. Contoh: ∠AOB.

Nah, kalau sudut keliling merupakan daerah sudut yang dibatasi oleh dua tali busur yang berpotongan di satu titik pada lingkaran dan titik sudutnya terletak pada keliling lingkaran. Contoh: ∠ADB dan ∠ACB.

Udah tau bedanya?

Oke walaupun mereka beda, tapi mereka tuh nggak putus hubungan ya.

Ada hubungan antara sudut pusat dan sudut keliling lingkaran.

Kalau keduanya menghadap busur yang sama maka besar sudut pusat bakal sama dengan dua kalinya besar sudut keliling.

Baca Juga: Kedudukan Titik dan Garis Lurus terhadap Lingkaran

Oh ya, biar kamu makin kenal sama sudut keliling, ga ada salahnya kamu pelajari sifat dari sudut keliling yaa biar jadi bestiie!

a. Besar sudut keliling yang menghadap diameter lingkaran adalah 90°

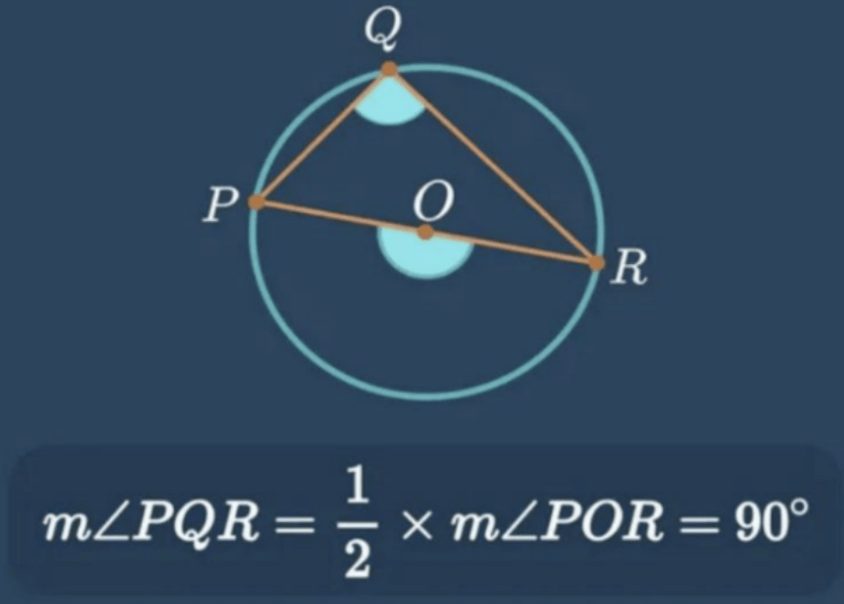
(sumber: Video Belajar Ruangguru)

b. Besar sudut-sudut keliling yang menghadap busur yang sama adalah sama besar

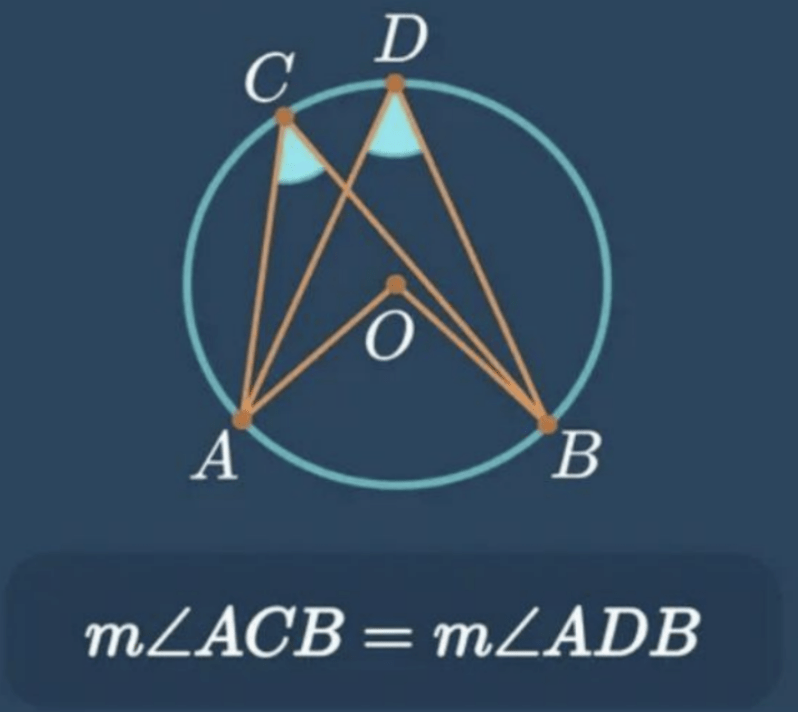
(sumber: Video Belajar Ruangguru)

c. Jumlah besar sudut-sudut yang berhadapan pada segi empat tali busur (Segi empat yang sisinya tali busur) adalah 180°

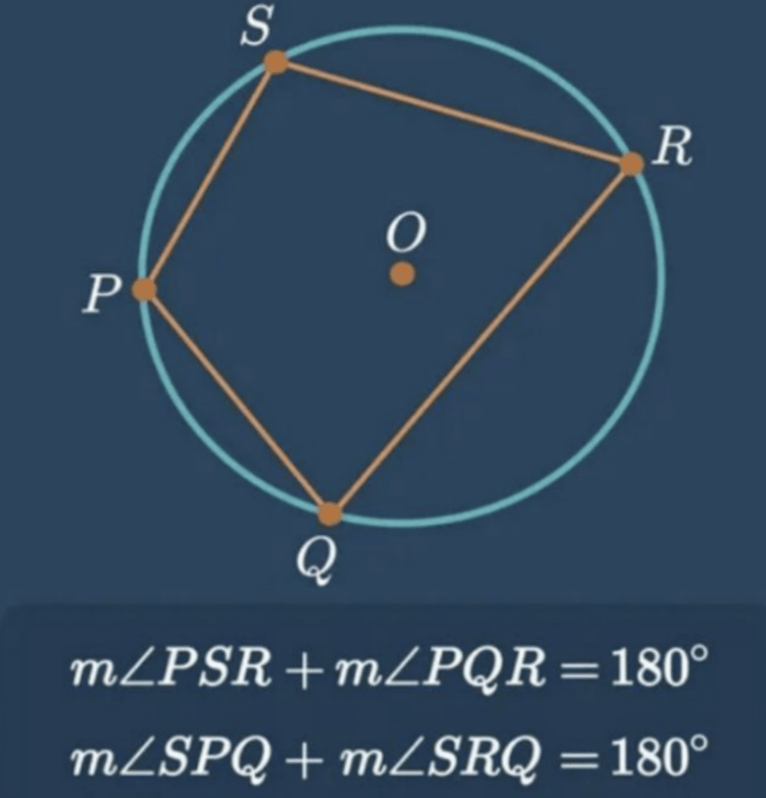
(sumber: Video Belajar Ruangguru)

Contoh Soal!

Sebuah lingkaran memiliki besar ∠ABC = 60° dan ∠AOC = (4x – 12)°. Berapakah nilai x pada lingkaran tersebut?

Pembahasan:

Diketahui:

Sudut keliling lingkaran = ∠ABC = 60°

Sudut pusat lingkaran = ∠AOC = (4x – 12)°

Ditanya: Nilai x …?

Jawab:

∠AOC = 2 × ∠ABC
(4x – 12)° = 2 × 60°
(4x – 12)° = 120°
4x = 120° + 12°
4x = 132°
x = 33°

Jadi, didapat nilai x-nya adalah 33º. Sehingga, kita bisa tahu juga nih nilai sudut pusat lingkaran tersebut, yaitu:

∠AOC = (4x – 12)°
∠AOC = (4(33) – 12)°
∠AOC = (132 – 12)° = 120°

Berdasarkan perhitungan di atas, didapat nilai ∠AOC = 120°

3. Rumus Panjang Busur dan Luas Juring

Busur dalam lingkaran itu bukan seperti busur yang digunakan untuk memanah ya guys.

Busur bukan juga istri dari Pak Sur, hehehe.

Dalam matematika, busur adalah garis lengkung yang terletak pada lengkungan lingkaran dan menghubungkan dua titik pada keliling lingkaran. Contohnya garis lengkung AB.

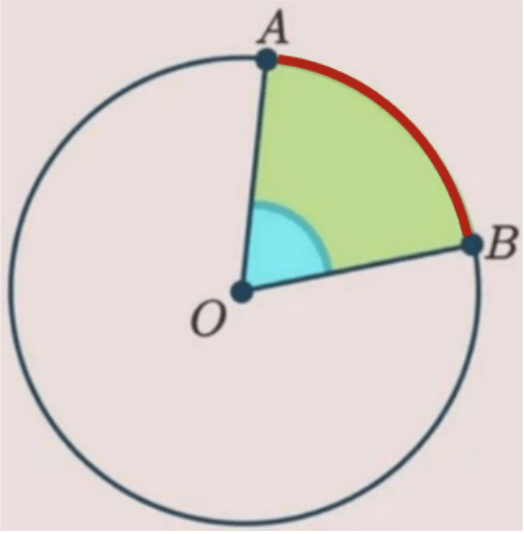
(sumber: Video Belajar Ruangguru)

Nah kalau juring itu daerah di dalem lingkaran yang dibatasi oleh dua jari-jari dan satu busur lingkaran. Contohnya luas juring AOB.

Perlu kamu ketahui nih, buat cari panjang suatu busur dan luas juring, ada kaitannya sama sudut pusat lingkaran yang udah kamu pelajari di awal. Jangan kamu lupain ya.

Untuk mencari panjang busur lingkaran, kamu bisa dapetin dengan konsep perbandingan antara besar sudut pusat yang menghadap busur dan panjang busur dibanding dengan  besar sudut lingkaran dan panjang keliling lingkaran. Konsepnya kalau disederhanakan langsung kaya gini nih.

Sementara untuk mendapatkan luas juring, kamu bisa menggunakan konsep perbandingan antara besar sudut pusat yang menghadap busur dan luas juring yang dibatasi busur, dibanding dengan  besar sudut lingkaran dan luas lingkaran. Rumusnya jadi seperti ini:

Dari dua konsep panjang busur dan luas juring di atas, kamu bisa membuat hubungan spesial dari keduanya yang bisa bantu kamu menyelesaikan suatu masalah.

Kalau misal diketahui busur dan juringnya punya sudut pusat yang sama, terus ditanyakan salah satunya, kamu tinggal selesaikan menggunakan konsep perbandingan kaya gini.

Baca Juga: Cara Mencari Kemiringan (Gradien) pada Garis Lurus

Tapi kalau misalnya busur atau juringnya punya sudut yang berbeda, kamu juga bisa tetap menggunakan konsep perbandingan dengan membandingkan sudut pusat yang diketahui.

(sumber: Video Belajar Ruangguru)

4. Rumus Luas Tembereng

Apa itu tembereng?

Tembereng adalah daerah yang dibatasi oleh tali busur dan busur lingkaran. Dari gambar di atas, temberengnya adalah daerah yang berwarna biru.

Kalau mau cari luas tembereng, sebenarnya itu guampang pol, kalau udah diketahui luas juring dan luas segitiga. Karena kalau kamu liat lagi gambarnya tuh, luas daerah tembereng AD itu sama kaya luas juring di atasnya, yaitu luas juring AOD yang dikurangi luas segitiga AOD.

Nah, itu tadi penjelasan lengkap mengenai cara menghitung unsur-unsur lingkaran. Semoga kamu semakin paham yah! Kalau kamu pengen tambah ngerti penjelasan dalam artikel ini, gabung yuk di ruangbelajar.

Ada banyak video belajar pake animasi, rangkuman kece, latian soal yang mudah sampe menantang, dan bahkan ada game nya juga yang bisa bikin kamu cinta buat belajar.

Referensi:

Raharjo M, Setiawan A. (2018) Matematika SMP/MTs Kelas VIII. Jakarta: Erlangga