Kedudukan Titik dan Garis Lurus terhadap Lingkaran | Matematika Kelas 11

Yuk, belajar tentang kedudukan titik dan garis lurus terhadap lingkaran! Selain teori, di artikel ini ada latihan soalnya juga, lho!

—

Di tingkat SMP, kamu sudah belajar mengenai lingkaran. Mulai dari mengenal berbagai macam bagian-bagian lingkaran, sampai dengan cara menghitung luas bangunnya. Pada lingkaran, terdapat yang namanya titik pusat dan juga jari-jari. Nah, ada yang masih inget nggak, pengertian dari keduanya?

Titik pusat merupakan suatu titik yang berada tepat di tengah lingkaran. Sementara itu, jari-jari lingkaran merupakan garis lurus yang menghubungkan titik pusat dengan satu titik pada garis lengkung lingkaran. Supaya lebih kebayang nih, coba deh kamu perhatikan lingkaran berikut!

P : pusat lingkaran, r : jari-jari lingkaran (Sumber: rumuspintar.com)

Dari gambar bisa terlihat ya, pusat itu letaknya di tengah-tengah, sedangkan jari-jari merupakan garis yang menghubungkan titik pusat dengan tepi lingkaran. Sekarang, kakak ada beberapa pertanyaan, nih. Bagaimana jika terdapat satu titik yang terletak bukan di pusat lingkaran? Atau, bagaimana jika ada garis lurus pada lingkaran yang tidak kita ketahui dengan jelas, apakah garis itu memotong lingkaran atau bersinggungan dengan lingkaran?

Nah, pertanyaan-pertanyaan itulah yang akan kita bahas pada artikel kali ini, yaitu mengetahui kedudukan atau letak suatu titik dan garis lurus terhadap lingkaran. Oke, langsung saja kita simak pembahasannya berikut ini!

Kedudukan Titik terhadap Lingkaran

Kedudukan titik terhadap lingkaran terbagi menjadi tiga kondisi, yaitu titik terletak di dalam lingkaran, titik terletak di luar lingkaran, dan titik terletak pada garis lengkung lingkaran. Sebenarnya, letak titik pada lingkaran ini dapat kita ketahui dengan mudah apabila keduanya digambarkan pada bidang Kartesius. Tapi, cara itu kurang efektif karena memerlukan waktu yang cukup lama. Apalagi, jika digunakan di ujian nanti.

Eits, tenang aja! Ada cara lain yang bisa kita gunakan untuk mengetahui kedudukan titik-titik tersebut tanpa harus menggambarnya, yakni dengan menggunakan rumus persamaan lingkarannya sebagai berikut:

• Jika pusatnya P (0,0) dan jari-jarinya r, maka bentuk persamaannya x² + y² = r²
• Jika pusatnya P (a,b) dan jari-jarinya r, maka bentuk persamaannya (x – a)² + (y – b)² = r²
• Jika pusatnya 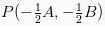dan jari-jarinya r = 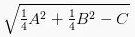, maka bentuk persamaannya x² + y² +Ax + By + C = 0

Ada tiga macam bentuk umum persamaan lingkaran. Penentuan letak suatu titik pada lingkaran tergantung dari masing-masing bentuk persamaannya.

1. Kedudukan titik terhadap lingkaran dengan bentuk x² + y² = r²

Pada bentuk persamaan x² + y² = r², lingkaran memiliki titik pusat di O (0,0) dan panjang jari-jari r. Misalkan terdapat suatu titik, yaitu Q (x₁, y₁). Kedudukan titik Q terhadap lingkaran x² + y² = r² adalah sebagai berikut:

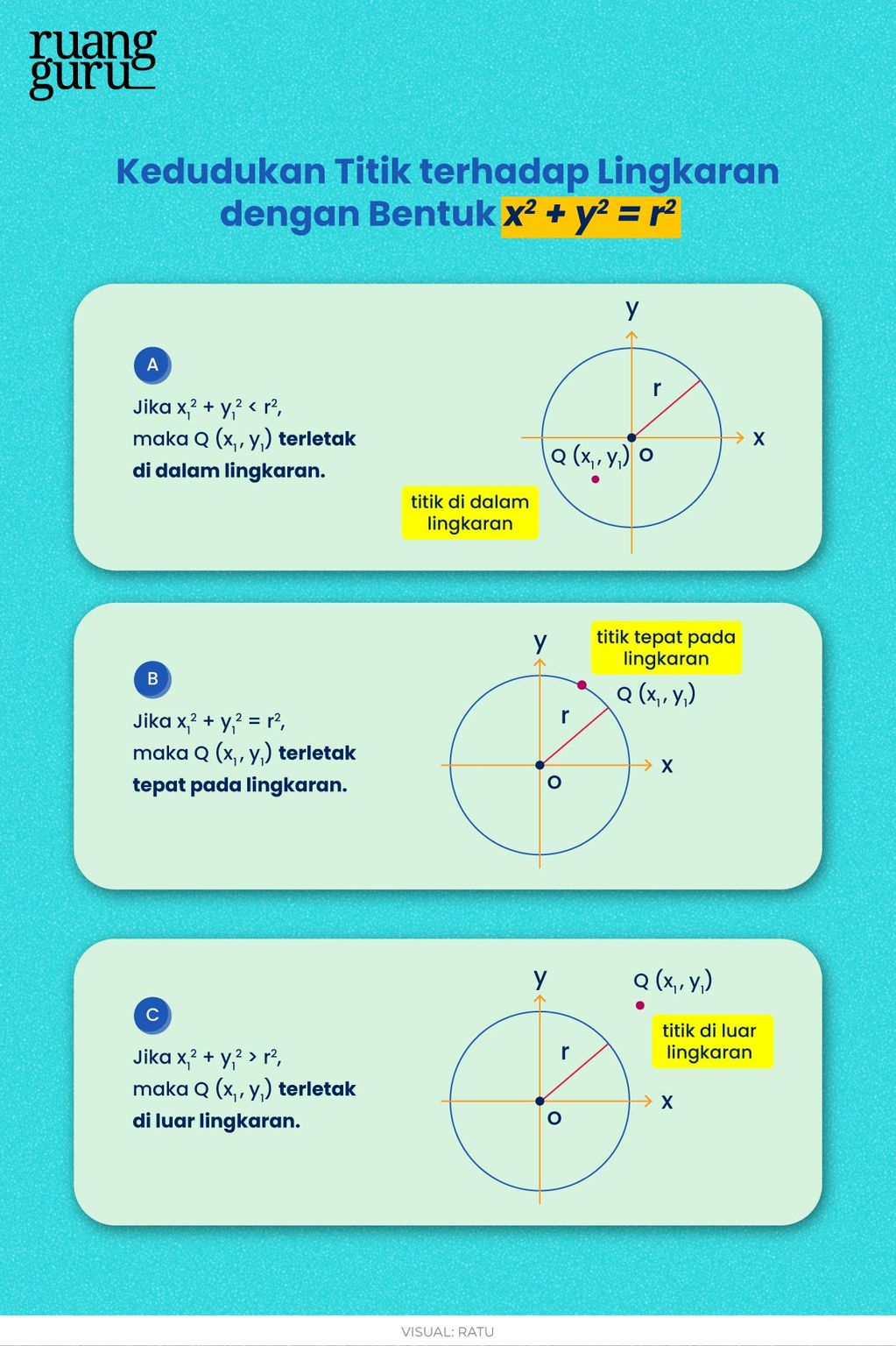
Supaya kamu lebih mudah memahami maksud dari rumus di atas, yuk kita coba kerjakan beberapa contoh soal di bawah ini.

Contoh soal:

1. Tentukanlah kedudukan atau posisi titik (5,2) terhadap lingkaran x² + y² = 25!

2. Titik (8,p) terletak tepat pada lingkaran x² + y² = 289 apabila p bernilai?

Pembahasan:

1. Pada persamaan x² + y² = 25 diketahui nilai r² = 25. Untuk menentukan kedudukan titik (5,2) terhadap lingkaran x² + y² = 25, kita bisa langsung mensubstitusikan titik tersebut ke dalam persamaan lingkarannya.

Sehingga (x, y) = (5, 2) diperoleh:

x² + y² = 52 + 22

              = 25 + 4

              = 29

Karena 29 > 25. Jadi, titik (5,2) terletak di luar lingkaran x² + y² = 25

2. Syarat agar titik (8, p) terletak pada lingkaran x² + y² = 289, maka ketika titik (8, p) disubstitusikan ke persamaan lingkarannya, harus sama dengan 289. Kalau kita substitusikan diperoleh:

x² + y² = 289 

8² + p² = 289

64 + p² = 289

p² = 225

p = √225

p = 15 atau -15

Jadi, agar titik (8, p) terletak tepat pada lingkaran x² + y² = 289, nilai p haruslah bernilai 15 atau -15.

Baca juga: 4 Metode Pembuktian Matematika

Eits, istirahat dulu bacanya sebentar ya. Punya PR susah dan bingung harus tanya kemana? Gampang, kamu bisa langsung kirim foto soal dan dapatkan jawabannya di Roboguru!

2. Kedudukan titik terhadap lingkaran dengan bentuk (x-a)² + (y-b)² = r²

Pada bentuk persamaan ini, lingkaran memiliki titik pusat di P (a,b) dan panjang jari-jari r. Misalkan, terdapat suatu titik, yaitu Q (x₁, y₁). Kedudukan titik Q terhadap lingkaran (x-a)² + (y-b)² = r² adalah sebagai berikut:

Contoh soal:

Tentukan kedudukan titik (3, 5) terhadap lingkaran dengan persamaan (x-3)² + (y-2)² = 16!

Pembahasan:

Seperti pada pembahasan soal nomor 1 sebelumnya, letak titik (3, 5) pada lingkaran (x-3)² + (y-2)² = 16 dapat kita ketahui dengan mensubstitusi titik tersebut ke dalam persamaan lingkaran,

sehingga

3 – 3² + 5 – 22 = 0² + 32

                           = 9

Karena 9 < 16, jadi titik (3, 5) terletak di dalam lingkaran x – 3² + y – 22 = 16

3. Kedudukan titik terhadap lingkaran dengan bentuk x² + y² + Ax + By + C = 0

Persamaan lingkaran dengan bentuk x² + y² + Ax + By + C = 0 memiliki:

• Titik pusat di
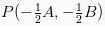
• Jari-jari r =

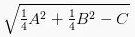
Sebenarnya, bentuk persamaan ini merupakan hasil penjabaran dari bentuk (x-a)² + (y-b)² = r².  Misalnya, terdapat suatu titik pada lingkaran, yaitu Q (x₁, y₁). Kedudukan titik Q terhadap lingkaran x² + y² + Ax + By + C = 0 adalah sebagai berikut:

Sekarang, kita coba kerjakan soal di bawah ini.

Contoh soal:

Tentukan nilai m agar titik (2, m) terletak di luar lingkaran x² + y² + 2x – 6y – 15 = 0!

Pembahasan:

Agar titik (2, m) berada di luar lingkaran x² + y² + 2x – 6y – 15 = 0, syarat yang harus dipenuhi adalah ketika titik (2, m) disubstitusikan ke pesamaan lingkarannya, maka diperoleh  x₁² + y₁² + Ax + By + C > 0. Oleh karena itu, kita substitusikan titik (2, m) ke dalam persamaan x² + y² + 2x – 6y – 15 = 0, menjadi sebagai berikut:

x² + y² + 2x – 6y – 15 > 0

2² + m² + 4 – 6m -15 > 0

4 + m² + 4 – 6m – 15 > 0

m² – 6m – 7 > 0

(m – 7)(m + 1) > 0

Nah, ternyata kita dapetnya pertidaksamaan nih, kalau begitu kita harus cari dulu pembuat nolnya, yaitu:

(m – 7)(m + 1) = 0

m = 7 atau m = -1

Kemudian, gambarkan ke garis bilangannya:

Karena tanda pertidaksamaannya >, maka daerah yang kita pilih adalah yang positif. Sehingga, nilai m yang memenuhi adalah m < -1 atau m > 7.

Jadi, agar titik (2, m) berada di luar lingkaran x² + y² + 2x – 6y – 15 = 0, nilai m yang memenuhi adalah m > 7 atau m > -1.

Nah, teman-teman, paham ya dengan penjelasan di atas? Sekarang, kita lanjut yuk ke bahasan tentang kedudukan garis lurus terhadap lingkaran. Cus, meluncuuurrr!!!

Baca juga: Konsep Limit Fungsi Aljabar dan Sifat-Sifatnya

Kedudukan Garis Lurus terhadap Lingkaran

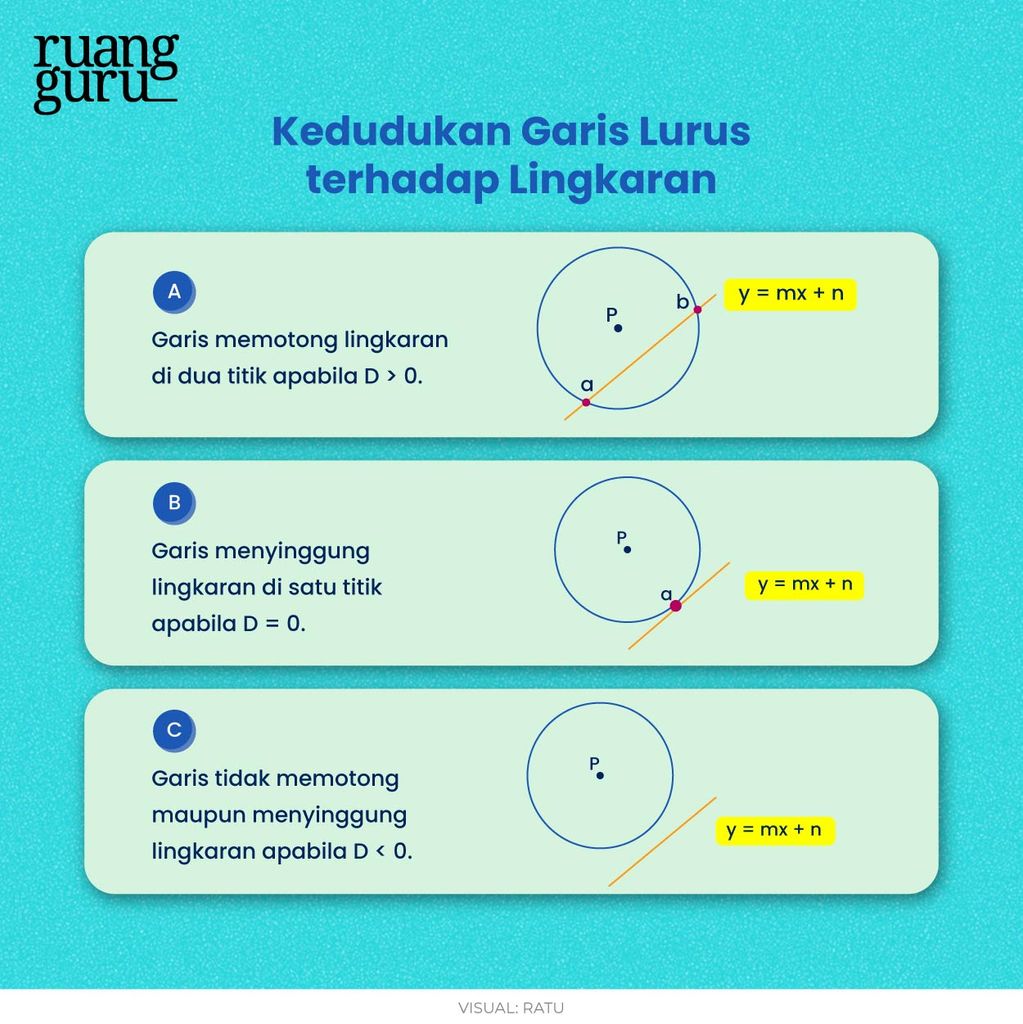
Sama halnya dengan pembahasan sebelumnya, kedudukan garis lurus terhadap lingkaran terbagi menjadi tiga kondisi, yaitu garis memotong lingkaran di dua titik berbeda, garis menyinggung lingkaran di satu titik, dan garis tidak memotong ataupun menyinggung lingkaran.

Misalkan, ada:

• Sebuah garis lurus dengan persamaan y = mx + n; dan
• Lingkaran dengan persamaan x² + y² + Ax + By + C = 0

Kedudukan garis lurus pada lingkaran dapat kita cari menggunakan nilai diskriminannya.

Diskriminan (D = b² – 4ac) diambil dari persamaan kuadrat yang merupakan hasil substitusi dari persamaan garis dengan persamaan lingkarannya.

Contoh soal:

Tentukan posisi garis y = 3x – 1 terhadap lingkaran x² + y² + 2x + 2y – 4 = 0!

Pembahasan:

Pertama, kita cari persamaan kuadrat dengan mensubstitusikan terlebih dahulu persamaan garis y = 3x – 1 ke dalam persamaan lingkaran x² + y² + 2x + 2y – 4 = 0, sehingga:

x² + (3x – 1)² + 2x + 2(3x – 1) – 4 = 0

x² + 9x² – 6x + 1 + 2x + 6x – 2 – 4 = 0

10x² + 2x – 5 = 0

Setelah kita peroleh persamaan kuadratnya, kita cari nilai diskriminannya sebagai berikut:

10x² + 2x – 5 = 0, a = 10, b = 2, c = -5.

D = b² – 4ac

D = 2² – 4(10)(-5)

D = 2² + 200

D = 222

Karena nilai diskriminannya adalah 222, dan 222 > 0, maka garis y = 3x – 1 memotong lingkaran x² + y² + 2x + 2y – 4 = 0 di dua titik.

Gimana, nih? Semoga kamu paham ya dengan penjelasan di atas. Nah, di bawah ini kakak masih ada beberapa latihan soal lagi yang bisa kamu kerjakan di rumah.

Oke, selesai sudah pembahasan kita kali ini. Kakak harap, artikel ini dapat membantumu dalam memahami materi tentang kedudukan titik dan garis lurus terhadap lingkaran. Ingat, belajar matematika itu harus banyak latihan soal ya, supaya materi yang kamu pelajari bisa lebih mudah terserap. Kamu bisa menemukan ribuan latihan soal lengkap dengan pembahasannya, di ruangbelajar lho! Yuk, meluncur ke sana sekarang!

Referensi: 

Sutrisna, Waluyo S. (2017). Konsep Penerapan Matematika SMA/MA Kelas XI. Jakarta: Bumi Aksara. 

Sumber Gambar:

Gambar ‘Pusat dan Jari-Jari Lingkaran’ [Daring]. Tautan: https://rumuspintar.com/wp-content/uploads/2019/09/Lingkaran.jpg (Diakses: 12 Januari 2021)

Artikel ini telah diperbarui pada 12 Januari 2022.