Cara Menentukan Persamaan Lingkaran dan Contohnya | Matematika Kelas 11

Artikel Matematika kelas 11 kali ini akan menjelaskan tentang cara menentukan persamaan lingkaran. Ingin tahu bagaimana penjelasannya? Simak artikel berikut yang juga menyajikan contoh soalnya lho.

—

Coba sekali-kali pas kamu lagi bantu-bantu cuci motor atau mobil, perhatikan bagian rodanya deh. Di mobil tuh, bagian tengah-tengah velg (logam/kaleng yang terpasang pada ban) biasanya ada logo perusahaan yang membuat mobil tersebut. Kalau kamu perhatikan, titik tengah dari logo tersebut pasti memiliki jarak yang sama jika ditarik ke sisi-sisi luar ban yang berbentuk lingkaran.

Nah, sebelumnya kamu sudah belajar tentang bangun datar kan. Lingkaran termasuk salah satu bentuk bangun datar lho. Hayoo, apa kamu masih ingat apa itu lingkaran?

Titik yang dimaksud dari pengertian tersebut ialah pusat lingkaran, dan jarak yang dimaksud ialah jari-jari.

Setelah tahu pengertian lingkaran, berikut dijelaskan mengenai persamaan dan unsur lingkaran. Ada dua hal penting yang harus kamu pahami di persamaan lingkaran, yakni jari-jari dan pusat lingkaran. Ada pun kaidahnya seperti berikut:

Baca Juga: Unsur-Unsur Lingkaran Ada Apa Saja, Ya?

Bentuk Umum Persamaan Lingkaran

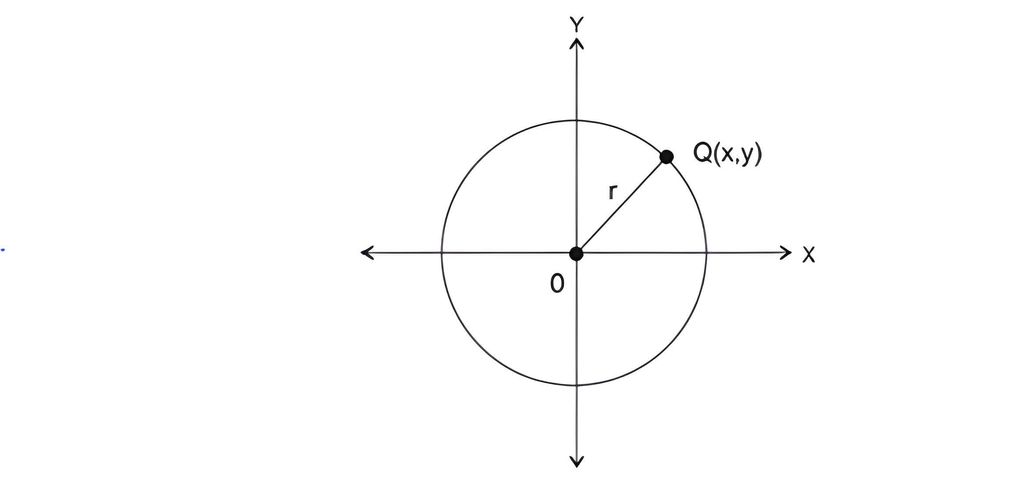
Jika pusatnya (0,0) dan jari-jari itu r, maka bentuk persamaannya x² + y² = r².

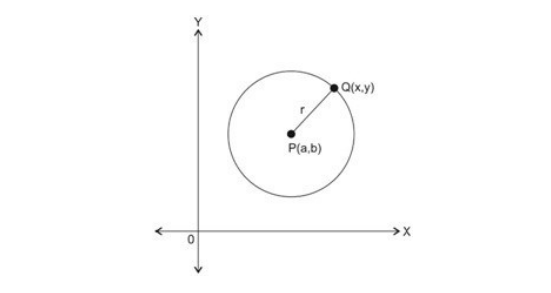
Jika pusatnya (a,b) dan jari-jari itu r, maka bentuk persamaannya (x – a)² + (y – b)² = r².

Cara Mencari Titik Pusat dan Jari-Jari dari Persamaan Lingkaran

Nah, terus gimana nih kalau kamu ingin mencari titik pusat dan jari-jari dari persamaan lingkaran yang diketahui. Gampang banget! Kamu bisa menggunakan dua pilihan cara, yakni:

Pertama, jika persamaannya (x – a)² + (y – b)² = r², maka pusatnya (a, b) dan jari-jarinya r.

Kedua, jika persamaannya x² + y² + Ax + Bx + C = 0, maka pusatnya 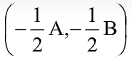 dan jari-jarinya .

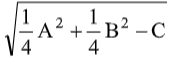Baca Juga: Rumus Menghitung Unsur-Unsur Lingkaran dan Contohnya

Contoh Soal Persamaan Lingkaran

Biar makin paham dengan materinya, kita latihan soal dulu, yuk! Kita kerjakan sama-sama, ya.

Sebuah lingkaran memiliki titik pusat (2, 3) dan berdiameter 8 cm. Persamaan lingkaran tersebut adalah…

1. x² + y² – 4x – 6y – 3 = 0
2. x² + y² + 4x – 6y – 3 = 0
3. x² + y² – 4x + 6y – 3 = 0
4. x² + y² + 4x + 6y + 3 = 0
5. x² + y² + 4x – 6y + 3 = 0

Jawaban: A

Pembahasan:

Karena d = 8, berarti r = 8/2 = 4, sehingga persamaan lingkaran yang terbentuk adalah:

(x – 2)² + (y – 3)² = 42

x² – 4x + 4 + y² -6y + 9 = 16

x² + y² – 4x – 6y – 3 = 0

Gimana nih penjelasan tentang cara menentukan persamaan lingkaran? Semoga bisa membuat kamu paham ya. Kalau masih bingung, kamu nggak perlu khawatir. Belajar lebih mudah dan asyik sekarang bisa di ruangbelajar for desktop lho. Install aplikasinya di laptop kamu dan tonton video belajar animasinya. Daftar sekarang juga yuk.

Referensi:

Sutrisna, Waluyo S. Konsep Penerapan Matematika SMA/MA Kelas XI. Jakarta: Bumi Aksara.