Cara Menyusun Persamaan dari Grafik Fungsi Kuadrat | Matematika Kelas 10

Di kelas 9, kamu sudah belajar sedikit mengenai fungsi kuadrat. Nah di kelas 10 ini, kamu akan belajar bagaimana caranya merumuskan fungsi kuadrat berdasarkan grafik. Penasaran? Simak penjelasannya berikut ini, ya!

—

Siapa di sini yang suka main game Angry Birds? Game yang sempat viral pada masanya itu, merupakan permainan di mana kita menembakkan burung menggunakan bantuan ketapel ke arah kastil musuh yaitu si babi hijau, supaya kastil mereka hancur.

Angry Birds (Sumber: giphy.com)

Kamu tahu nggak sih, pada game tersebut, burung yang kita lempar menggunakan ketapel akan membentuk lintasan parabola yang bentuknya seperti grafik fungsi kuadrat, lho!

Ciri-Ciri Grafik Fungsi Kuadrat

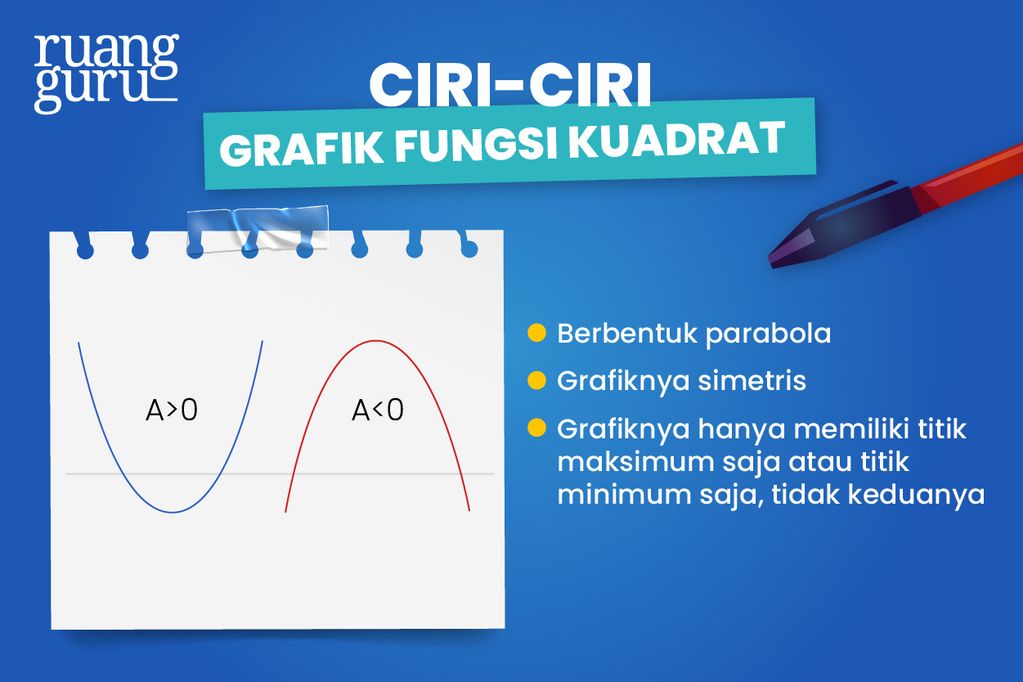
Grafik fungsi kuadrat memiliki beberapa ciri, di antaranya yaitu:

1. Berbentuk parabola

2. Grafiknya simetris

3. Hanya memiliki titik maksimum saja atau titik minimum saja, namun tidak keduanya

Nah, dari grafik fungsi kuadrat, kita bisa merumuskan fungsi kuadratnya lho! Gimana ya, caranya?

Eits, tapi sebelum masuk ke pembahasan itu, kita kilas balik sebentar yuk, ke materi fungsi kuadrat di kelas 9. Kamu masih ingat kan, tentang fungsi kuadrat? Kalau kamu lupa, coba cek videonya di ruangbelajar, deh!

Bentuk Umum Fungsi Kuadrat

Fungsi kuadrat merupakan aturan yang memasangkan semua anggota daerah asal tepat satu ke daerah kawan dengan pangkat pada variabel tertingginya adalah dua.

Baca Juga: Cara Menyusun Persamaan Kuadrat

Bentuk umum dari fungsi kuadrat yaitu f(x) = ax² + bx + c, dengan keterangan sebagai berikut:

Keterangan:

a = koefisien dari x², di mana a ≠ 0

b = koefisien dari x

c = konstanta

Nah, sekarang yuk, kita masuk ke pembahasan utama kita yaitu merumuskan fungsi kuadrat berdasarkan grafik!

—

Sampai sini, sudah mulai paham belum dengan materi cara mencari persamaan pada grafik fungsi kuadrat? Kalo masih ada poin-poin yang belum kamu mengerti, mending belajar sama ahlinya, deh. Belajar bareng kakak-kakak pengajar di Ruangguru Privat Matematika misalnya.

Belajar nggak cuma menyenangkan, tapi kamu juga bakal diajari konsepnya sampai paham! Para pengajar di Ruangguru Privat juga sudah terstandarisasi kualitasnya, loh. Kamu juga bisa pilih nih, mau diajarkan secara langsung (offline) atau daring (online). Fleksibel, kan? Untuk info lebih lanjut, cuss klik link berikut!

Cara Merumuskan Fungsi Kuadrat Berdasarkan Grafik

Sebelum merumuskan fungsi kuadrat berdasarkan grafik, kita harus lihat dulu nih, nilai apa yang diketahui pada grafik tersebut, karena rumus yang akan kita pakai tergantung dari nilai apa yang diketahui pada grafik.

Ada tiga macam rumus yang bisa kita pakai untuk merumuskan fungsi kuadrat berdasarkan grafik, yaitu:

1. Jika pada grafik diketahui 2 titik sembarang pada sumbu x, maka menggunakan rumus y = a(x – x₁)(x – x₂).
2. Jika pada grafik diketahui titik puncak (x_p, y_p) dan 1 titik sembarang, maka menggunakan rumus y = a(x – x_p)² + y_p.
3. Jika pada grafik diketahui 3 titik sembarang, maka menggunakan bentuk umum fungsi kuadrat yaitu y = ax² + bx + c, lalu gunakan eliminasi untuk mencari nilai a, b, dan c.

Supaya kamu lebih paham, coba perhatikan infografik berikut, ya!

Baca Juga: Yuk, Belajar Fungsi Komposisi & Contohnya, Lengkap!

Sekarang, kita lanjut mengerjakan latihan soal, yuk!

Contoh Soal Grafik Fungsi Kuadrat

Sekarang, kita kerjakan contoh soal, yuk! Coba kamu perhatikan grafik berikut:

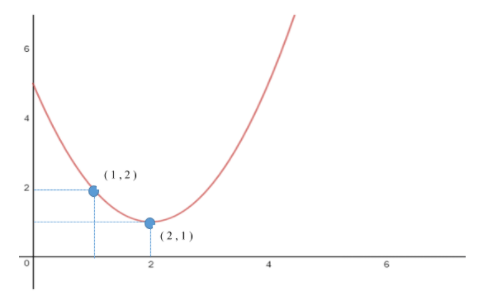
Dari grafik tersebut, diketahui titik puncak atau titik balik dari suatu fungsi kuadrat, yaitu di titik (2, 1). Selain itu, diketahui juga 1 titik sembarang yaitu (1, 2). Coba rumuskan fungsi kuadratnya!

Jawaban:

Diketahui dari soal bahwa:

• (x_p, y_p) = (2, 1)
• Titik sembarang = (1, 2)

Nah, sesuai penjelasan tadi, jika pada grafik diketahui titik puncak (x_p, y_p) dan 1 titik sembarang, maka kita menggunakan rumus:

y = a(x – x_p)² + y_p

Yuk, kita coba uraikan!

y = a(x – x_p)² + y_p

2 = a(1 – 2)² + 1

2 = a(-1)² + 1

2 = a(1) + 1

2 = a + 1

a = 2 – 1

a = 1

Karena titik puncaknya di (2, 1) dan nilai a = 1, maka fungsi kuadratnya:

y = a(x – x_p)² + y_p

y = 1(x – 2)² + 1

y = x² – 4x + 4 + 1

y = x² – 4x + 5

Selesai, deh! Jadi, dari grafik tersebut dapat kita rumuskan bahwa fungsi kuadratnya adalah f(x) = x² – 4x + 5.

—

Gimana? Gampang, kan? Kalau kamu ingin tahu bagaimana cara merumuskan fungsi kuadrat berdasarkan grafik menggunakan kedua rumus lainnya, kamu bisa cek penjelasannya di video belajar beranimasi yang ada di ruangbelajar, lho! Yuk, langganan sekarang!

Referensi:

Sinaga, B. dkk. (2017). Matematika untuk SMA/MA/SMK/MAK Kelas X Kurikulum 2013 Edisi Revisi 2017. Jakarta: Pusat Kurikulum dan Perbukuan, Balitbang, Kemendikbud.

Sumber Gambar:

GIF ‘Angry Birds’ [Daring]. Tautan: https://giphy.com/gifs/angry-birds-12OUZridgOdMOI (Diakses: 10 Agustus 2021)