Cara Menentukan Persamaan Garis Lurus dan Contohnya | Matematika Kelas 8

Artikel Matematika kelas 8 ini menjelaskan tentang cara menentukan persamaan garis lurus serta cara menggambar grafik dari persamaan garis lurus. Selain itu, ada juga beberapa contoh soal untuk meningkatkan pemahaman kamu terhadap materi.
—
“Bang, permen seribu dapet berapa?”
“Empat biji, dek”
“Perasaan kemarin seribu dapet lima, bang. Kok naik? Sekarang, dua ribu berapa?”
“Ya delapan lah, dek”
“Bukannya sekarang dua ribu dua empat, yak? Hiya… hiya… hiya…!”
.gif)
“Udah bawel, garing lagi!” (sumber: tenor.com)
Pernah nggak sih kamu ngalamin hal itu? Bukan ngerjain abang-abang tukang jualan, ya. Tapi ngerasain yang namanya kenaikan harga barang.
Perasaan, beberapa waktu yang lalu, beli permen seribu bisa dapet lima. Sekarang, udah naik aja harganya. Jadi cuma dapat empat, deh.
Sebenarnya, kenaikan harga barang itu hal yang biasa lho karena harga bahan baku semakin lama juga akan semakin mahal. Ya… sisi positifnya sih uang jajan kamu kan jadi bakal bertambah. Tadinya cuma 5.000 sehari, sekarang bisa 10.000, deh. Lumayan, tuh!
Oke, coba kita buat grafik dari masalah kenaikan harga permen tersebut ke dalam bidang Kartesius. Kita misalkan saja harga permen sebagai variabel y dan tahun sebagai variabel x.
Kemudian, kita pilih selang tahun antara 2011-2019. Kita perkirakan harga permen di tahun 2011 seharga Rp150/buah dan setiap dua tahun sekali, harga permen meningkat secara tetap sebesar Rp25/buah.
Jadi, kalo di tahun 2011 itu harga permen 150/buah, maka di tahun 2012 jadi 175/buah, setiap tahun selalu naik hingga mencapai harga Rp250/buah di tahun 2019.
Baca Juga: Cara Menyelesaikan Sistem Persamaan Linear Dua Variabel
Nah, hasil grafiknya akan seperti ini.
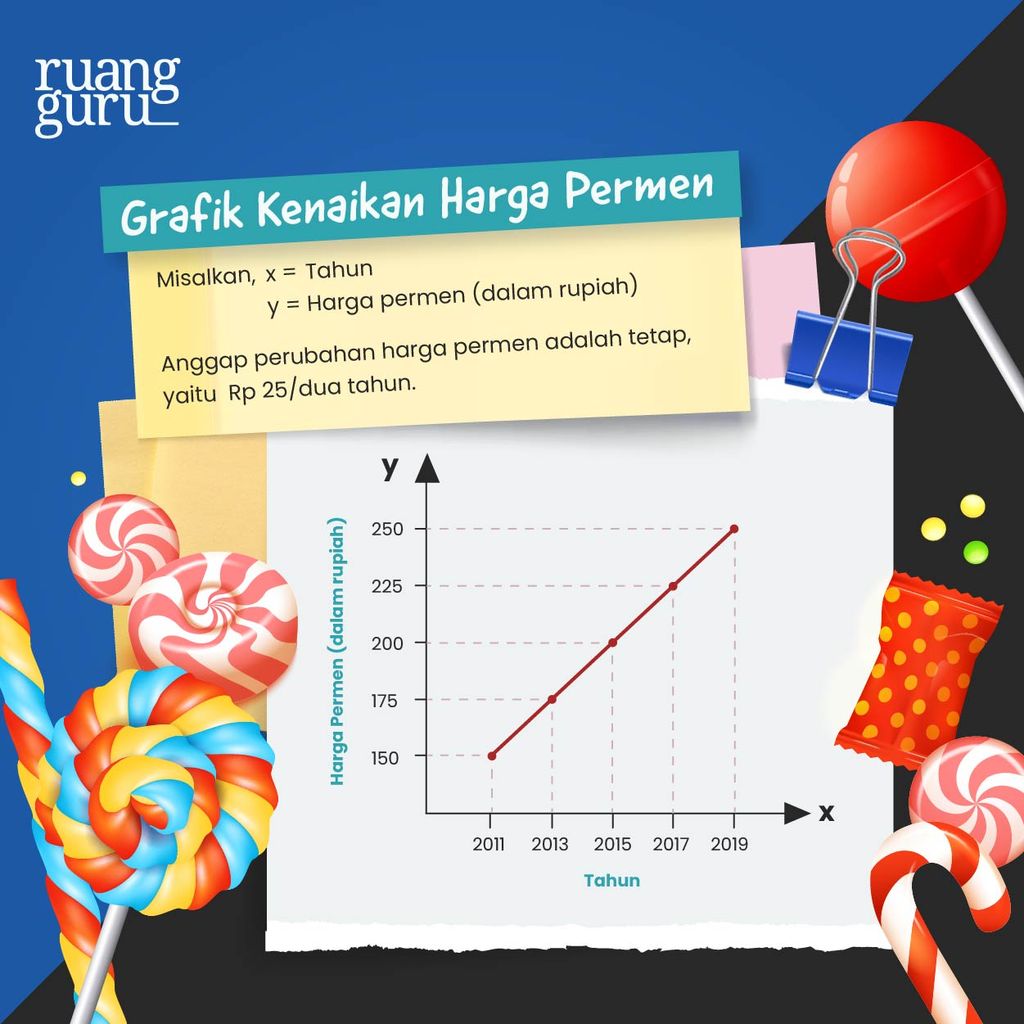
Ternyata, kurva yang terbentuk adalah linear (berbentuk garis lurus). Berdasarkan kurva tersebut, kamu bisa menentukan persamaan garis lurusnya, lho. Mau tau gimana caranya? Kuy, langsung aja disimak!
Mengenal Persamaan Garis Lurus
Sebelumnya, kita ketahui dulu yuk apa itu persamaan garis lurus. Persamaan garis lurus adalah persamaan yang membentuk garis lurus saat digambarkan dalam bidang Kartesius. Bentuk umum persamaan garis lurus adalah sebagai berikut:

Baca Juga: Cara Mencari Kemiringan (Gradien) pada Garis Lurus
Di sini, kamu harus ingat ya, namanya bentuk umum itu bukan berarti persamaan garis lurusnya akan selalu berbentuk seperti gambar di atas.
Tapi, secara umum, bentuknya akan memiliki dua variabel yang masing-masing variabelnya punya pangkat (orde) tertinggi satu. Contohnya, 2x + y = 4, 3y = x – 6, x + y – 2 = 0, dan masih banyak lagi. Bisa kamu lihat ya kalo variabel x dan variabel y itu pangkatnya satu.
Cara Menentukan Persamaan Garis Lurus
Ada dua hal yang perlu diperhatikan saat ingin membuat persamaan garis lurus. Pertama, kamu harus tahu nilai gradien dari garis tersebut dan kedua, kamu harus tahu sedikitnya satu titik yang dilalui garis itu.
Berikut ini merupakan dua kondisi yang dapat dicari tahu bentuk persamaan garis lurusnya. Hmm… kira-kira, grafik di atas termasuk kondisi yang mana, ya?
1. Jika diketahui gradien dan satu titik yang dilalui garis
Misalnya, suatu garis melalui sebuah titik, yaitu (x1, y1). Kamu dapat menentukan persamaan garis lurusnya dengan rumus:
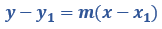
Contoh:
Tentukan persamaan garis yang bergradien 3 dan melalui titik (-2,-3)!
Penyelesaian:
Diketahui m = 3 dan (x1, y1) = (-2,-3). Sehingga,
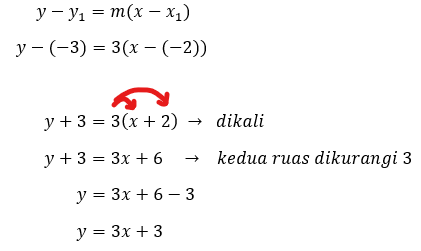
Jadi, persamaan garis lurusnya adalah y = 3x + 3.
2. Jika diketahui dua titik yang dilalui garis
Misalnya, suatu garis melalui dua buah titik, yaitu (x1, y1) dan (x2, y2). Kamu bisa menggunakan rumus di bawah ini untuk mengetahui persamaan garisnya.
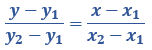
Ternyata, kalau kamu perhatikan, kondisi ini cocok untuk mencari persamaan garis lurus dari grafik kenaikan harga permen di atas. Coba yuk kita cari tahu persamaan garis lurusnya bersama-sama.
Pada gambar grafik kenaikan harga permen, diketahui kalau garis melalui beberapa titik. Misalnya, kita pilih dua titik dari beberapa titik tersebut, yaitu (x1, y1) = (2011, 150) dan (x2, y2) = (2019, 250). Sehingga,
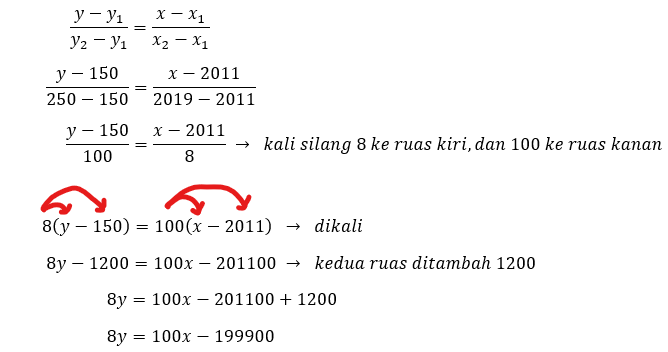
Jadi, persamaan garis lurus dari grafik kenaikan harga permen di atas adalah 8y = 100x – 199900.
Paham, ya?
Nah, sekarang kamu sudah mengetahui cara menentukan persamaan garis lurus dari dua buah kondisi yang diketahui, ya. Lalu, bagaimana jika kamu diminta untuk menggambarkan grafik dari suatu persamaan garis lurus? Yuk, simak langkah-langkahnya di bawah ini!
Baca Juga: Macam-Macam Ukuran Pemusatan Data: Mean, Median, Modus
—
Gimana? Apakah kamu sudah mulai paham dengan materi persamaan garis lurus? Kalo masih ada poin-poin yang belum kamu mengerti, mending belajar sama ahlinya, deh. Belajar bareng kakak-kakak pengajar di Ruangguru Privat Matematika misalnya.
Belajar nggak cuma menyenangkan, tapi kamu juga bakal diajari konsepnya sampai paham! Para pengajar di Ruangguru Privat juga sudah terstandarisasi kualitasnya, loh. Kamu juga bisa pilih nih, mau diajarkan secara langsung (offline) atau daring (online). Fleksibel, kan? Untuk info lebih lanjut, cuss klik link berikut!
Cara Menggambar Grafik dari Persamaan Garis Lurus
Terdapat tiga langkah dalam membuat grafik dari persamaan garis lurus. Supaya kamu lebih mudah memahami, kita langsung masuk ke contoh soalnya aja ya.
Contoh Soal:
Gambarlah grafik dari persamaan garis lurus y = 3x – 9!
Pembahasan:
1. Cari titik potong di sumbu x
Cara mencari titik potong pada sumbu-x adalah dengan membuat variabel y menjadi 0.

Jadi, saat y = 0, nilai x yang dihasilkan adalah 3. Sehingga, diperoleh titik potong di sumbu-x adalah (3,0).
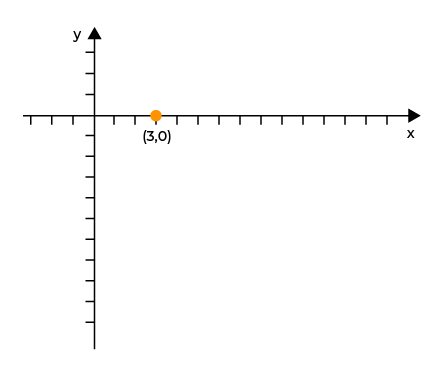
2. Cari titik potong di sumbu y
Tidak jauh berbeda dengan cara mencari titik potong pada sumbu-x, untuk mencari titik potong di sumbu-y, kita harus mengganti variabel x menjadi 0.

Jadi, saat x = 0, nilai y yang dihasilkan adalah -9. Sehingga, diperoleh titik potong di sumbu-y adalah (0,-9).
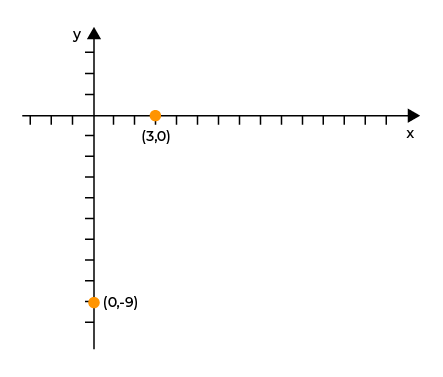
3. Gambar garis yang menghubungkan titik potong tersebut
Setelah diperoleh dua buah titik potongnya, kita bisa tarik garis lurus yang menghubungkan kedua titik potong tersebut. Sehingga, hasilnya akan seperti ini.
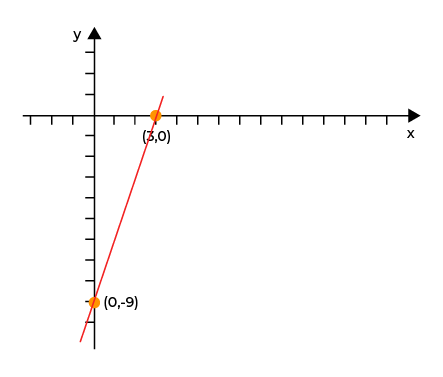
Gimana? Mudah kan caranya. Oh iya, untuk lebih memudahkan kamu dalam mengerjakan soal-soal yang berkaitan dengan persamaan garis lurus, artikel ini sudah merangkum rumus-rumus di atas tadi, lho! Spesial buat kamu. Ehe~

Yo! Apa tanggapan kamu setelah membaca artikel ini? Semoga segala kebingungan kamu terhadap materi persamaan garis bisa berkurang, ya.
Sekilas informasi aja nih, materi persamaan garis lurus ini puenting banget untuk dipahami. Kenapa? karena soalnya sering sekali keluar di ujian, loh.
Nah, kalau kamu merasa artikel ini kurang lengkap, kamu bisa tonton penjelasan lebih lengkapnya lagi di ruangbelajar. Belajar jadi lebih menyenangkan dengan video belajar beranimasi.
Referensi:
As’ari A.R, Tohir M, Valentino E, Imron Z, Taufiq I. (2017) Matematika SMP/MTs Kelas VIII Semester 1. Jakarta: Kementerian Pendidikan dan Kebudayaan
Sumber foto:
GIF ‘Orang Marah’ [Daring]. Tautan: https://tenor.com/view/glare-scowl-annoyed-ronswanson-parksandrec-gif-4601682 (Diakses: 23 Desember 2020).





















