Rumus dan Cara Menghitung Mean, Median, Modus | Matematika Kelas 8

Artikel Matematika kelas 8 ini membahas mengenai pengertian ukuran pemusatan data, yang meliputi mean, median, modus, cara menentukan nilai mean, median, modus, dan masing-masing contoh soalnya.

—

Banyak orang suka menyembunyikan nilai ujiannya supaya orang lain nggak tau, seakan-akan nilai ujian tuhh rahasiaaa banget.

Pernah nggak sih temenmu nanya nilai ujian yang udah kamu rahasiakan banget? Terus pada akhirnya, kamu kasih tau dengan harapan dia nyebutin nilainya juga. Eh, ternyata dia ikut ujian susulan, jadi nilainya belum keluar deh.

Mungkin, kamu dan yang lain ngerasa, “nggak adil banget sih, kan dia udah tau nilai kita semua” atau “yahh… kalo kita nanya nilainya, pasti nggak bakal dikasih tau nih”.

Padahal, kamu bisa tau nilainya loh, tapi dengan syarat, kamu harus tau nilai rata-rata kelas. Tenang, nanti bakal aku lanjut bahas caranya. Nah, ngomongin tentang rata-rata, sebenarnya menghitung nilai rata-rata udah pernah dipelajari waktu SD dulu. Di SMP ini, kamu bakal belajar yang sedikit lebih kompleks, tapi tetap seru kok!

Rata-rata (mean) termasuk salah satu contoh ukuran pemusatan data. Hah, apa itu ukuran pemusatan data?

Pengertian ukuran pemusatan data adalah sembarang ukuran yang menjadi pusat dari beberapa data, dengan syarat data-data ini sudah diurutkan dari yang terkecil ke terbesar, atau sebaliknya. Simpelnya, dari beberapa data terurut, akan diperoleh suatu nilai yang menjadi nilai pusat atau perwakilannya.

Sebenarnya, ukuran pemusatan data itu nggak cuma ada rata-rata (mean) aja. Ada beberapa contoh ukuran pemusatan data lain, seperti modus dan median. Kita akan bahas satu persatu tiga macam ukuran pemusatan data, dimulai dari rata-rata dulu, ya.

Mean (Rata-Rata)

Rata-rata bisa kita sebut juga dengan mean. Rata-rata (mean) adalah suatu bilangan yang mewakili sekumpulan data. Rata-rata (mean) dilambangkan dengan simbol x̄ (dibaca x bar).

Kita bisa menghitung nilai rata-rata atau mean dari data tunggal dan data tunggal berkelompok atau berfrekuensi. Apa ya bedanya data tunggal dan data tunggal berkelompok?

Jadi kalo data tunggal, kita mengumpulkan atau memperoleh data apa adanya (bisa berurutan atau acak) dan tidak mengelompokkannya ke tabel frekuensi. Contoh data tunggal:

Nilai Ujian Matematika kelas VIII-A

5   9   7   8   6   5
6   8   9   5   7   8
7   9   8   6   6   5
8   8   6   5   7   5
7   8   6   5   5   7

Angka 5,6,7,8,9 dari data di atas disebut datum atau bisa dibilang masing-masing angka yang ada pada suatu data. 

Baca Juga: Mengenal Statistika dalam Diagram Penyajian Data

Cara Mencari Rata-Rata (Mean)

Untuk memperoleh nilai rata-rata, kita bisa membagi jumlah semua nilai atau datum-nya dengan banyaknya data. Nah, ini dia rumus mencari mean-nya:

Kebayang nggak sih gimana ribet dan panjangnya tulisan, kalo misalnya kamu harus ngumpulin nilai dari 200 orang? Nggak efisien banget dong. Solusinya, kita bisa mengelompokkan data atau nilainya dengan tabel frekuensi, atau bisa juga dibilang data tunggal berkelompok. Misalnya:

Untuk rumus mencari nilai rata-rata data tunggal berkelompok, bisa ditulis seperti ini:

Kita coba yuk latihan soal pakai rumus-rumus itu!

Contoh Soal Mencari Rata-Rata (Mean)

Data nilai ulangan harian IPA kelas VIII-1. Berapa banyak siswa di kelas itu yang nilainya lebih dari rata-rata?

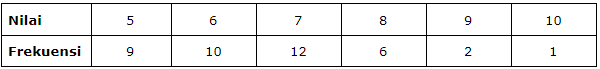
Penyelesaian:

Cari dulu nilai rata-rata pakai rumus data tunggal berkelompok:

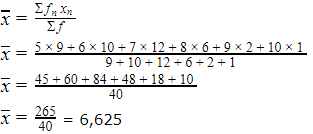
Diperoleh nilai rata-ratanya adalah 6,625. Karena yang ditanya di soal itu banyak siswa yang nilainya di atas rata-rata, maka nilainya ada 7 sampai 10. Kalau kita total semua jumlah siswanya, ada sebanyak 21 siswa.

Median (Data Tengah)

Data tengah atau median adalah datum yang letaknya di tengah suatu kumpulan data, tapi dengan syarat datanya sudah diurutkan dari yang terkecil sampai terbesar.

Median dapat dilambangkan dengan Me. Nah, kunci untuk mencari nilai median ini, kamu bisa perhatikan jumlah data yang ada, misal datanya itu ganjil atau genap. Karena, beda jumlah data, beda juga rumus mediannya.

Baca Juga: Cara Menyelesaikan Sistem Persamaan Linear Dua Variabel (SPLDV)

Cara Mencari Median

Seperti yang sudah disebutkan sebelumnya, untuk mencari nilai median, punya rumus yang berbeda. Setiap rumus ada perbedaannya, bergantung dari banyaknya data. Berikut rumus mencari median berdasarkan data ganjil dan data genap:

Untuk data berjumlah ganjil, kamu bisa langsung ambil angka tengahnya. Tapi, untuk data berjumlah genap, akan ada 2 angka yang ditengah. Jadi, supaya kamu bisa peroleh nilai mediannya, harus pakai rumus yang berbeda. Nah, kalo kamu masih bingung dan nggak kebayang pakai rumusnya, mendingan kita langsung bahas soal yuk!

Contoh Soal Mencari Median

Soal 1

Median dari data: 7, 8, 8, 9, 4, 3, 7, 9, 5, 7, 6, 5, 6 adalah …

Penyelesaian:

Ingat ! urutkan nilainya dari terkecil sampai terbesar

3, 4, 5, 5, 6, 6, 7, 7, 7, 8, 8, 9, 9 (n =13 termasuk data ganjil). Maka, kamu bisa menggunakan rumus median untuk data ganjil, yaitu:

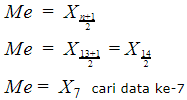
Sehingga, diperoleh nilai mediannya adalah 7.

Soal 2

Median dari data berikut adalah …

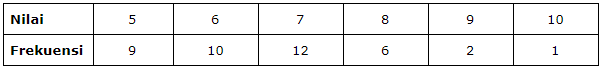
Penyelesaian:

Kemudian, hitung dulu banyaknya data yang ada. Karena datanya genap, maka kamu bisa menggunakan rumus median untuk data genap, yaitu:

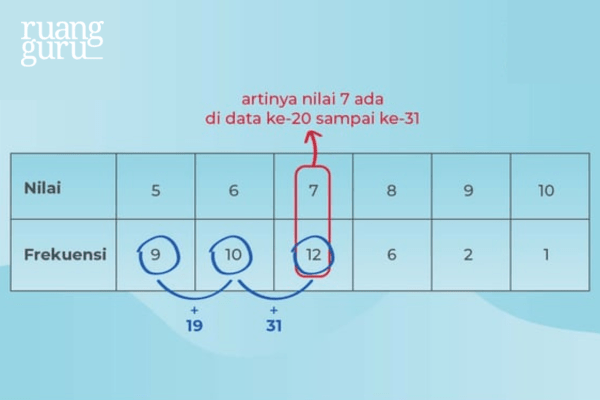
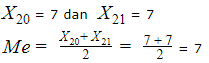
Jadi diperoleh nilai mediannya, yaitu 7.

Modus (Nilai yang Sering Muncul)

Nah, untuk macam ukuran pemusatan data yang ketiga ini, pasti udah nggak asing lagi, kan? Yap, modus adalah nilai yang paling sering muncul. Jadi, dalam kelompok data, jika ada angka yang paling banyak ada (paling sering muncul), itu lah yang dinamakan modus. Biasanya, modus dilambangkan dengan Mo.

Kalau data yang kamu peroleh merupakan data tunggal berkelompok atau data yang dikelompokkan ke dalam tabel, maka kamu bisa langsung lihat datum atau nilai dengan frekuensi paling tinggi. Tapi, kalo data tunggal biasa, kamu bisa gunakan tabel turus/ tally. Biar kamu paham kita ke contoh soal ya!

Contoh Soal Mencari Modus

Modus dari data berikut adalah:

102, 108, 106, 107, 108
105, 107, 105, 108, 106
106, 106, 107, 102, 105
105, 102, 106, 105, 106
107, 106, 105, 106, 102
105, 107, 107, 106, 105
106, 106, 105, 107, 102

Penyelesaian:

Nah, karena data di atas merupakan data tunggal biasa, agar lebih mudah, buat dalam bentuk tabel turus seperti ini:

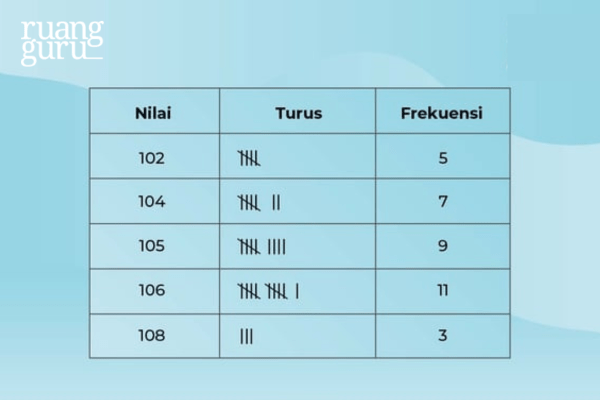
Kemudian, kalau kita lihat, data yang paling sering muncul adalah 106 karena nilai frekuensinya paling tinggi, yaitu 11. Jadi, modus dari data itu adalah 106.

Nah, kita udah bahas 3 ukuran pemusatan data nih. Sesuai janji di awal, kita bakal bahas cara mencari nilai salah satu siswa jika diketahui rata-rata nilai kelasnya. Caranya itu mirip banget sama soal di bawah ini, jadi pahami ya!

Baca Juga: Bagaimana Cara Menghitung Teorema Pythagoras?

Wah, seru banget kan bahasan materi mean, median, dan modus ini. Soal-soal ukuran pemusatan data ini tuh bervariasi banget. Selain harus paham konsep, kamu juga harus terbiasa hitung cepat dan tepat.

Caranya gimana tuhh supaya bisa hitung cepat dan tepat? Kamu harus perbanyak latihan, nah makanya setelah baca artikel ini langsung aja asah pemahaman dan kemampuan hitung kamu di ruangbelajar. Soal-soalnya bagus banget dijadikan latihan dan bisa mempertajam pemahaman kamu. Selamat belajar!

Referensi:

Kurniawan, (2013) Mandiri Matematika Untuk Kelas SMP/MTs Kelas VIII. Jakarta: Erlangga.