Yuk, Belajar 5 Jenis Permutasi dalam Teori Peluang | Matematika Kelas 12

Yuk, sama-sama kita belajar jenis-jenis permutasi dalam teori peluang! Ada apa saja, ya?

—

Setelah kamu belajar tentang aturan perkalian dan faktorial dalam teori peluang, sekarang kita akan lanjut belajar mengenai permutasi. Apa itu permutasi? Nah, permutasi adalah susunan unsur berbeda yang dibentuk dari n unsur, diambil dari n unsur atau sebagian unsur. Permutasi dapat dikelompokkan menjadi beberapa macam. Dalam artikel ini, kita akan belajar tentang jenis permutasi dalam teori peluang. Kira-kira apa saja ya jenis-jenis permutasi itu? Yuk, simak artikel berikut!

Rumus-rumus permutasi dalam teori peluang

1. Permutasi dari n elemen, tiap permutasi terdiri dari n elemen

Jika ada unsur yang berbeda, diambil n unsur, maka banyaknya susunan (permutasi) yang berbeda dari n unsur tersebut adalah: 

Contoh:

Untuk menyambut sebuah pertemuan delegasi negara yang dihadiri oleh lima negara, panitia akan memasang kelima bendera dari lima negara yang hadir. Banyak cara panitia menyusun kelima bendera tersebut adalah …

Jawab:

Dari lima bendera yang ada, berarti n = 5, maka banyak susunan bendera yang mungkin yaitu:

5! = 5.4.3.2.1 = 120 cara.

Baca juga: Rumus Bunga Majemuk dan Cara Menghitungnya

2. Permutasi n elemen, tiap permutasi terdiri dari r unsur dari n elemen dengan r ≤ n

Untuk semua bilangan positif n dan r, dengan r ≤ n, banyaknya permutasi dari n objek yang diambil r objek pada satu waktu adalah:

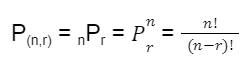
rumus permutasi ini memiliki syarat, yaitu urutan harus diperhatikan, ya!

Contoh:

Banyak cara untuk memilih seorang ketua, sekertaris dan bendahara dari 8 siswa yang tersedia adalah…

Jawab:

Banyak siswa, n = 8

Ketua, sekretaris dan bendahara (banyak pilihan objek), r = 3

Maka:

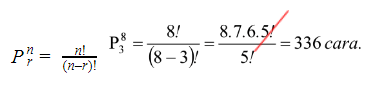
3. Permutasi dari n unsur yang mengandung p.q dan r unsur yang sama

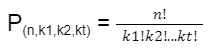
Keterangan:

n    = banyaknya elemen seluruhnya

k₁  = banyaknya elemen kelompok 1 yang sama

k₂  = banyaknya elemen kelompok 2 yang sama

…

k_t   = banyaknya elemen kelompok kt yang sama

t = 1,2,3,…

Contoh:

Banyak cara untuk menyusun dari kata ”BASSABASSI” adalah…

Jawab:

Dari kata ”BASSABASSI”, banyak huruf (n) = 10

k₁ = huruf B = 2

k₂ = huruf A = 3

k₃ = huruf S = 4

k₄ = huruf I = 1

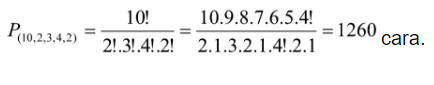
Baca juga: Istilah-Istilah Data Tunggal dalam Matematika

4. Permutasi Siklis

Permutasi siklis adalah permutasi melingkar (urutan melingkar).

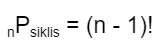
Contoh:

Dari 5 orang anggota keluarga akan duduk mengelilingi sebuah meja bundar, banyak cara susunan yang dapat dibuat dari 5 orang tersebut adalah…

Jawab:

Banyak orang (n) = 5, maka :

₅P_siklis = (5 – 1)! = 4! = 4.3.2.1 = 24 cara.

5. Permutasi berulang dari n unsur, tipe permutasi terdiri dari k unsur

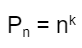
Contoh:

Banyak susunan 3 bilangan dari angka-angka 1, 2, 3, 4, 5 dan 6 adalah…

Jawab:

Banyak susunan 3 bilangan, berarti bilangan ratusan, k = 3
Banyak angka yang akan disusun, n = 6
Banyak susunan 3 bilangan dari angka 1, 2, 3, 4, 5, dan 6:

P₆ = 6³ = 216 susunan.

Oke, setelah kamu memahami perbedaan dari 5 jenis permutasi dan contoh soalnya, sekarang, coba kamu kerjakan beberapa latihan soal permutasi berikut ini, yuk!

Latihan Soal Permutasi

1. Ada berapa cara bila 4 orang siswa (misal: a, b, c, d) menempati tempat duduk yang akan disusun dalam suatu susunan yang teratur?

2. Suatu kelompok ekskul tari yang terdiri dari 3 siswa laki-laki dan 5 siswa perempuan akan memilih 3 orang pengurus. Berapa cara yang dapat dibentuk dari pemilihan jika pengurus terdiri dari 2 siswa laki-laki dan 1 siswa perempuan.

3. Dalam sebuah kantong terdapat 7 kelereng. Berapa banyak cara mengambil 4 kelereng dari kantong tersebut?

—

Sekarang sudah mengerti kan tentang jenis permutasi? Pada artikel selanjutnya, kamu bisa melanjutkan belajar tentang teori peluang yang fokus pada pembahasan kombinasi dan binomial newton. 

Masih bingung tentang permutasi? Yuk belajar bersama dengan video animasi yang keren hanya di ruangbelajar!

Sumber Referensi: 

Sharma S. N, Widiastuti N, Himawan C, dkk (2017) Jelajah Matematika SMA Kelas XII Program Wajib. Jakarta:Yudisthira

Artikel diperbarui 30 Agustus 2022.