Pengertian dan Istilah-istilah dalam Himpunan | Matematika Kelas 7

Memahami pengertian dan istilah dalam himpunan merupakan langkah awal untuk menguasai konsep himpunan ke tahap yang lebih lanjut. Yuk, kita pelajari di artikel Matematika kelas 7 ini!

—

Pernah nggak kamu ikut suatu perkumpulan di sekolah? Misalnya, klub basket, kelompok tari, atau komunitas pencinta Matematika? Nah, setiap perkumpulan itu punya anggotanya masing-masing, kan? Ada yang ikut klub basket karena suka olahraga, ada juga yang ikut kelompok melukis karena hobinya menggambar.

Kalau kamu perhatikan, setiap perkumpulan tersebut berisi orang-orang dengan kesamaan tertentu. Nah, dalam Matematika, hal seperti ini disebut himpunan. Misalnya, kalau ada “Himpunan Siswa Gemar Melukis” berarti di himpunan tersebut berisi orang-orang yang sama-sama suka melukis.

Kali ini, kita akan belajar tentang konsep himpunan. Melalui konsep ini, kita bisa lebih mudah memahami cara mengelompokkan sesuatu berdasarkan kesamaannya. Yuk, kita pelajari lebih lanjut tentang apa itu himpunan dan istilah-istilah penting di dalamnya!

Visualisasi Himpunan (sumber: blog.dinus.ac.id)

Pengertian Himpunan dalam Matematika

Kamu tahu nggak, apa itu himpunan? Secara sederhana, himpunan adalah kumpulan benda atau objek yang bisa kita jelaskan dengan jelas. Artinya, kita bisa tahu dengan pasti apakah sesuatu termasuk dalam himpunan itu atau tidak.

Baca Juga: Hubungan Antar Himpunan Matematika & Contohnya

Misalnya, himpunan siswa kelas 7B, berarti sudah pasti isinya semua siswa yang ada di kelas 7B aja. Jadi, kita bisa dengan mudah menentukan siapa yang termasuk di dalamnya.

Nah, tapi kalau himpunan siswa paling pintar di sekolah. “Paling pintar” itu kan bisa beda-beda menurut orang. Jadi anggotanya tidak bisa ditentukan secara pasti. Kalau begitu, itu bukan himpunan.

Yuk, lanjut kita pelajari contoh-contoh lainnya supaya kamu makin paham tentang apa itu himpunan!

Contoh Himpunan:

1. Himpunan hewan karnivora.
2. Himpunan siswa perempuan di kelas 7.
3. Himpunan bilangan asli.
4. Himpunan bilangan prima antara 10 dan 40.

Contoh Bukan Himpunan:

1. Himpunan lukisan yang menarik (karena arti kata menarik berbeda-beda menurut setiap orang).
2. Himpunan orang pintar (karena tidak ada ukuran pasti untuk mengukur kepintaran seseorang).
3. Himpunan warna yang bagus (karena arti kata bagus berbeda-beda menurut setiap orang).

Cara Menyatakan Himpunan

Sekarang kamu sudah tau kan kalau himpunan itu merupakan sesuatu yang dapat dinyatakan dengan jelas. Nah, misalnya, kamu sudah tahu nih bahwa himpunan bilangan-bilangan prima antara 10 dan 40 adalah 11, 13, 17, 19, 23, 29, 31, 37. Lalu, bagaimana ya caranya menyatakan suatu himpunan?

Ternyata, ada beberapa cara untuk menuliskan himpunan agar lebih mudah dipahami. Dalam matematika, himpunan bisa dinyatakan dengan tiga cara, yaitu:

1. Menyatakan Himpunan dengan Kata-kata

Kalau cara ini, kita tinggal menggunakan kalimat biasa untuk menjelaskan himpunan. Contoh: Himpunan bilangan-bilangan prima antara 10 dan 40 adalah 11, 13, 17, 19, 23, 29, 31, 37.

2. Menyatakan Himpunan dengan Notasi Pembentuk Himpunan

Untuk cara kedua dan ketiga, kita perlu tahu dulu aturan penulisan himpunan yang benar. Karena dalam matematika, simbol dan tanda itu penting banget supaya artinya tidak salah. Supaya kamu nggak bingung, perhatikan penjelasan di bawah ini, ya!

Aturan Cara Penulisan Himpunan:

• Nama himpunan ditulis dengan huruf kapital, misalnya A, B, C, dan seterusnya.
• Anggota himpunan ditulis di dalam kurung kurawal { }.
• Setiap anggota dipisahkan dengan tanda koma (,).
• Jika anggota himpunan terlalu banyak atau tidak bisa dituliskan semua, gunakan tanda titik-titik ( … ). Contoh: B = {2, 4, 6, 8, …, 100}
• Simbol ϵ dibaca “anggota dari” dan digunakan untuk menunjukkan bahwa sesuatu termasuk dalam himpunan. Contoh: 11 ϵ A (artinya 11 adalah anggota himpunan A)
• Simbol ∉ dibaca “bukan anggota dari” dan menunjukkan bahwa sesuatu tidak termasuk dalam himpunan. Contoh: 15 ∉ A (artinya 15 bukan anggota himpunan A)

Oke, lanjut yaaa. Cara menyatakan himpunan dengan notasi pembentuk himpunan akan menggunakan simbol dan tanda untuk menunjukkan syarat keanggotaan suatu himpunan.

Contoh:

A = {x | x adalah bilangan prima antara 10 dan 40}

Artinya: A adalah himpunan yang anggotanya (x) merupakan bilangan prima antara 10 dan 40. Tanda “|” dibaca “dengan syarat” atau “sedemikian sehingga”.

Baca Juga: Pengertian dan Contoh Bilangan Bulat 

3. Menyatakan Himpunan dengan Mendaftarkan Anggota-anggotanya

Cara ketiga ini yang biasa sering digunakan. Kita tinggal menuliskan semua anggota himpunan tersebut di dalam kurung kurawal, di mana setiap anggotanya dipisahkan oleh tanda koma.

Contoh:

A = {11, 13, 17, 19, 23, 29, 31, 37}

Istilah-Istilah Penting dalam Himpunan

Dalam himpunan, kita juga bakal sering menemui beberapa istilah tertentu. Misalnya semesta, himpunan kosong, dan sebagainya. Yuk, simak masing-masing perbedaannya!

1. Kardinalitas

Kardinalitas adalah banyaknya anggota yang berbeda dalam suatu himpunan. Dengan kata lain, kardinalitas menunjukkan jumlah elemen atau anggota yang ada di dalam himpunan tersebut.

Untuk menuliskan banyaknya anggota himpunan, kita menggunakan notasi n. Biasanya ditulis seperti ini:

n(A) dibaca “banyaknya anggota himpunan A”

Contoh 1:

Nah, coba perhatikan contoh berikut:

A = { huruf-huruf pembentuk kata “cermat” }

Untuk membentuk kata cermat, kita membutuhkan huruf c, e, r, m, a, dan t. Dengan kata lain, A = {c, e, r, m, a, t}.

Dari huruf-huruf tersebut, ternyata nggak ada huruf yang sama atau berulang, jadi jumlah hurufnya ada 6.

Maka, banyaknya anggota himpunan A adalah n(A) = 6.

Contoh 2:

Sekarang, perhatikan lagi contoh di bawah:

B = { huruf-huruf pembentuk kata “semangat” }

Kalau dari segi Bahasa Indonesia, huruf-huruf pembentuk kata semangat itu terdiri dari s, e, m, a, n, g, a, dan t. Tapi, beda konsepnya dengan himpunan. Meskipun huruf “a” muncul dua kali dalam kata “semangat”, dalam himpunan kita tetap tulis satu kali aja. Karena dalam himpunan, setiap anggota hanya dihitung satu kali, meskipun muncul berulang.

Jadi, B = {s, e, m, a, n, g, t}

Maka, banyaknya anggota himpunan B adalah n(B) = 7.

2. Himpunan Semesta

Himpunan Semesta (Sumber: www.acsu.buffalo.edu)

Secara sederhana, himpunan semesta adalah himpunan yang berisi semua anggota atau objek yang sedang dibicarakan. Jadi, semua himpunan lain yang sedang kita bahas berada di dalam himpunan semesta.

Himpunan semesta biasanya dilambangkan dengan huruf S. Anggota-anggota dalam himpunan semesta bisa berbeda-beda, tergantung pada konteksnya.

Contoh:

Kalau kita sedang membahas tentang himpunan bilangan genap dan bilangan ganjil antara 1 sampai 10, maka himpunan semestanya (S) adalah semua bilangan dari 1 sampai 10.

S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

Dari himpunan semesta ini, kita bisa membentuk himpunan lain, yaitu:

Himpunan bilangan genap → A = {2, 4, 6, 8, 10}

Himpunan bilangan ganjil → B = {1, 3, 5, 7, 9}

Nah, sekarang kamu bisa lihat bahwa himpunan A dan B itu bagian dari himpunan semesta S. Itulah sebabnya disebut “himpunan semesta”, karena mencakup semua anggota yang sedang kita bicarakan.

3. Himpunan Kosong

Himpunan kosong adalah himpunan yang tidak memiliki satu pun anggota di dalamnya. Jadi, nggak ada apa pun yang bisa dimasukkan ke dalam himpunan itu. Himpunan kosong bisa ditulis dengan notasi { } atau ∅ (dibaca: “phi”).

Contoh:

Kamu diminta menyebutkan nama hari yang berawalan huruf “Z”. Coba pikir, ada nggak nama hari yang awalnya dari Z? Nggak ada, kan? Karena nggak ada, berarti himpunannya kosong, dan bisa ditulis:

E = { } atau E = ∅

Artinya, himpunan E tidak memiliki anggota.

Tapi, jangan sampai menulis himpunan kosong seperti ini: E = {0}

Karena {0} itu artinya ada satu anggota, yaitu angka 0. Sedangkan himpunan kosong sama sekali tidak punya anggota.

Jadi ingat ya, perbedaannya:

• { } atau ∅ → tidak ada anggota sama sekali
• {0} → ada anggota, yaitu angka 0

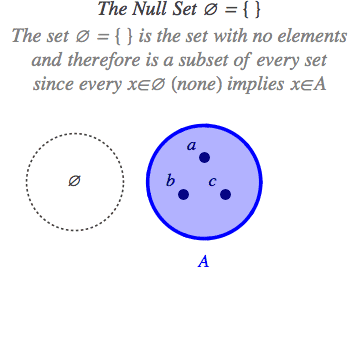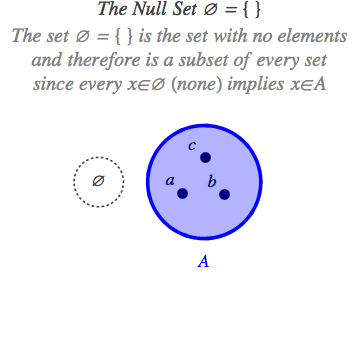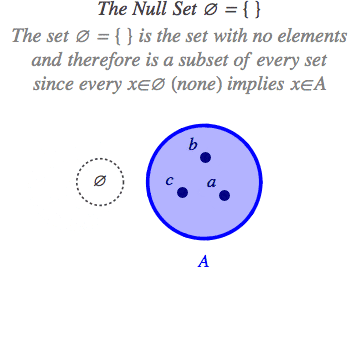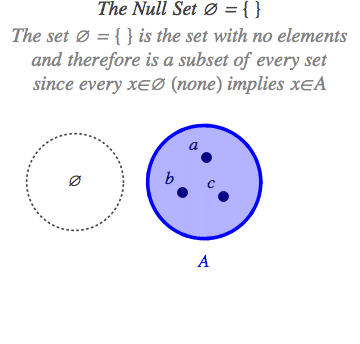Himpunan Kosong (sumber: MarchSchilder.com)

Baca Juga: Penjelasan Lengkap KPK dan FPB, Apa Bedanya Ya?

Wah, seru banget kan belajar tentang himpunan? Nah, biar makin paham dan pintar, kamu bisa lanjut belajar lewat video animasi seru di ruangbelajar. Di sana, kamu nggak cuma nonton penjelasan materi, tapi juga bisa latihan soal-soal interaktif yang bikin belajar jadi lebih mudah dan menyenangkan. Yuk, tunggu apa lagi? Buruan download aplikasi Ruangguru dan rasakan sendiri serunya belajar dengan cara baru! 🚀

Referensi:

As’ari A.R, Tohir M, Valentino E, Imron Z, Taufiq I. (2017) Matematika SMP/MTs Kelas VII Semester I. Pusat Kurikulum dan Perbukuan, Balitbang, Kemendikbud

Sumber foto:

Ilustrasi ‘Himpunan’ [Daring]. Tautan: https://student.blog.dinus.ac.id/ayupuspita/2018/11/15/himpunan-matematika-diskrit/ (Diakses: 21 Desember 2020)

Ilustrasi ‘Himpunan Semesta’ [Daring]. Tautan: https://www.acsu.buffalo.edu/~mbschild/Media-Advanced/Media-Advanced.html (Diakses: 21 Desember 2020)

Ilustrasi ‘Himpunan Kosong’ [Daring]. Tautan: https://www.acsu.buffalo.edu/~mbschild/images.html (Diakses: 21 Desember 2020)