Mengenal Matriks: Pengertian, Jenis, dan Transpose | Matematika Kelas 11

Kamu tahu apa itu matriks? Di artikel Matematika kelas 11 ini, kita akan mengupas konsep matriks meliputi pengertian, jenis-jenis, serta transpose matriks. Simak baik-baik, ya!

—

Kamu pasti pernah menghadapi masalah yang berkaitan dengan angka dan data. Contoh kecilnya aja, saat kamu dan teman-temanmu lagi mau makan bersama. Biasanya kan, biar nggak ribet dan lupa, semua pesanan dicatat di kertas, ya. Tapi, kalo pesanannya banyak dan ribet, lumayan ngebingungin juga nggak sih nyatetnya mau gimana. Kayak yang waktu itu sempat ramai di sosial media, nih.

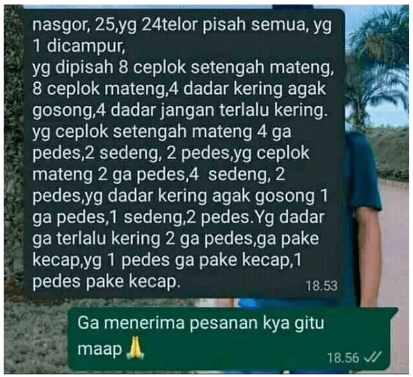
Perkara pesan nasi goreng (Sumber: suara.com)

Ya pantes abangnya nolak. Kamu aja yang sekali baca belum tentu paham. Iya apa iya? Ckckck… (geleng-geleng kelapa).

Sebenarnya, masalah di atas tuh bisa lho dibikin simpel dan gampang buat dipahami. Salah satunya pakai tabel. Nih, kalo aku buat ke dalam tabel, dengan barisnya menyatakan tingkat kepedasan dan kolomnya menyatakan telor, jadinya kayak gini.

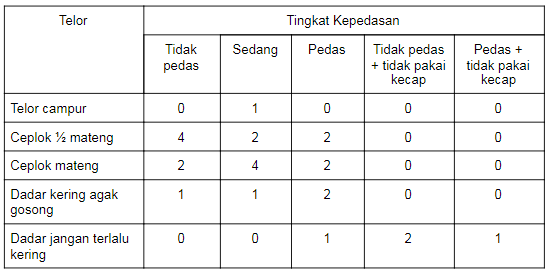
Karena si sender nggak kasih keterangan tuh, pesanan nasi goreng yang telornya dicampur rasanya pedas atau nggak, jadi aku asumsiin aja rasanya sedang. Gimana, kalo dibuat tabel kayak gini, jadi jauh lebih gampang kan buat dimengerti sama abang nasi gorengnya? Hueheheheh 😛

Nah, kamu tau nggak sih, ternyata, tabel di atas bisa dibuat ke bentuk yang lebih sederhana lagi lho, yaitu seperti ini:

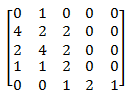
Urutan angka-angkanya sama. Cuma keterangan baris dan kolomnya aja yang dihilangkan. Terus, angka-angka tersebut diberi tanda kurung di sisi kanan dan kirinya. Kalo dalam Matematika, bentuk tersebut dinamakan matriks.

—

Sudah tahu belum, di Aplikasi belajar Ruangguru, ada fitur Drill Soal yang berisi kumpulan contoh soal latihan beserta pembahasannya, loh. Pas banget kan buat mempersiapkan diri kamu dalam menghadapi ujian nanti. Yuk, klik banner di bawah ini untuk coba fitur Drill Soal! 

Pengertian Matriks

Matriks adalah sekumpulan bilangan yang disusun berdasarkan baris dan kolom, serta ditempatkan di dalam tanda kurung. Nah, tanda kurungnya ini bisa berupa kurung biasa “( )” atau kurung siku “[ ]”, ya. Suatu matriks diberi nama dengan huruf kapital, seperti A, B, C, dan seterusnya.

Oh iya, kamu tau kan bedanya baris dan kolom? Baris itu susunannya horizontal atau ke samping, sedangkan kolom susunannya vertikal atau dari atas ke bawah.

Misalnya nih, matriks di atas tadi, kita beri nama matriks A. Maka,

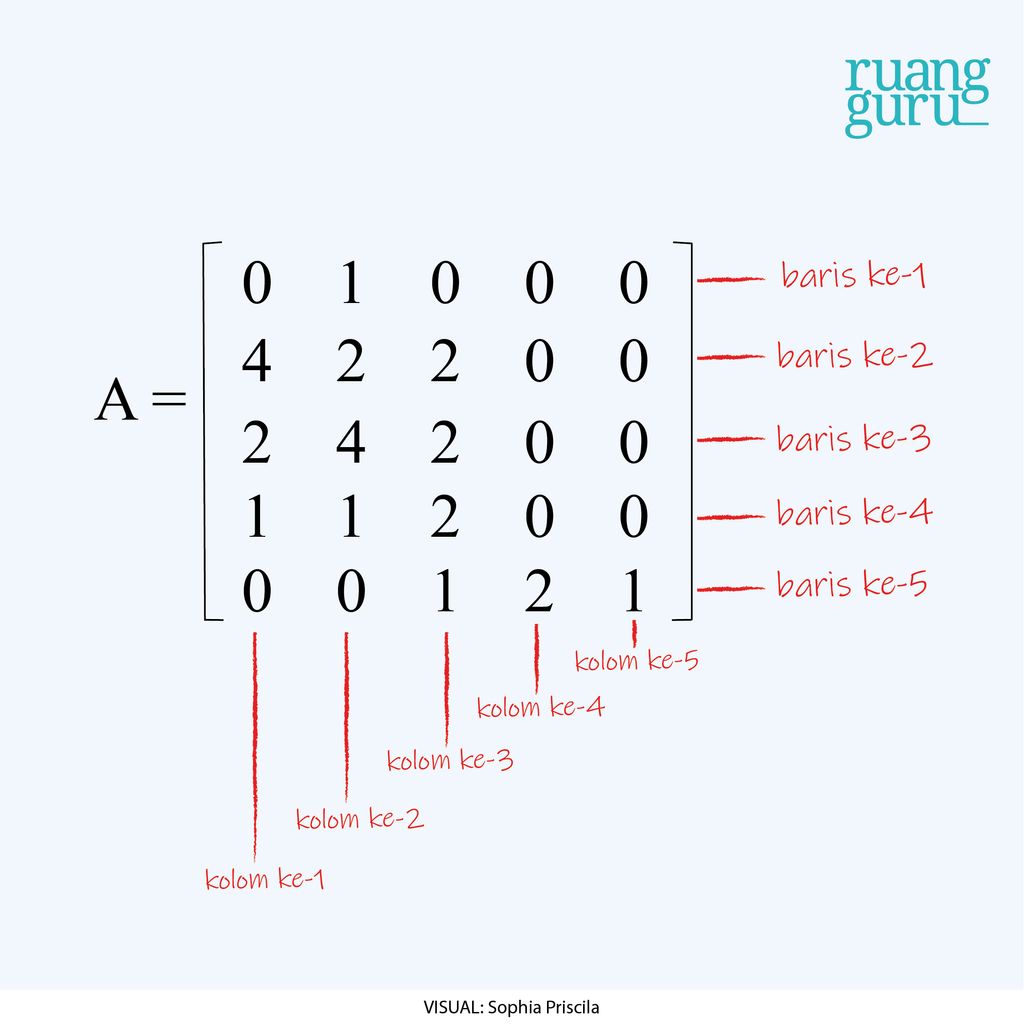
Penamaan baris dan kolom dibuat urut, ya. Jadi, baris ke-1 dimulai dari atas, urut ke bawah. Sementara itu, kolom ke-1 dimulai dari kiri ke kanan.

Baca Juga: Konsep Limit Fungsi Aljabar dan Sifat-sifatnya

Ordo dan Elemen Matriks

Matriks itu punya ukuran, guys. Ukuran matriks disebut ordo. Ordo matriks ini berdasarkan dari banyaknya baris dikali banyaknya kolom pada matriks. Jadi, kalo suatu matriks A memiliki m baris dan n kolom, maka matriks A tersebut berukuran (berordo) m x n. Supaya lebih sederhana, kita bisa menulisnya dengan A_mxn.

Nah, masing-masing bilangan yang terdapat di dalam matriks disebut elemen matriks. Elemen-elemen matriks juga ada notasinya sendiri, lho. Kalo matriks dinotasikan dengan huruf kapital, maka elemen-elemen matriks dinotasikan dengan huruf kecil dan diberi indeks yang menyatakan letak baris dan kolomnya.

Misalnya nih, pada matriks A di atas, jumlah barisnya kan ada 5 dan jumlah kolomnya juga ada 5, maka ordonya adalah 5 x 5, atau bisa kita tulis A_5×5. Lalu, untuk elemen-elemen matriks A bisa dinotasikan dengan a_ij, yang menyatakan elemen matriks A pada baris ke-i dan kolom ke-j.

Supaya kamu nggak bingung, langsung simak contoh di bawah ini aja, yuk!

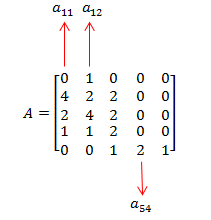
Kita ambil contoh a₁₁, a₁₂, dan a₅₄, seperti pada gambar.

• a₁₁ menyatakan elemen matriks A pada baris ke-1 kolom ke-1, nilainya adalah 0.
• a₁₂ menyatakan elemen matriks A pada baris ke-1 kolom ke-2, nilainya adalah 1.
• a₅₄ menyatakan elemen matriks A pada baris ke-5 kolom ke-4, nilainya adalah 2.

Gimana, paham kan cara bacanya?

Baca Juga: Operasi Aljabar Pada Matriks: Penjumlahan, Pengurangan & Perkalian

Jenis-Jenis Matriks

Selain punya ukuran (ordo), matriks juga terbagi menjadi beberapa bentuk yang mempunyai sifat khusus. Nah, beberapa jenis matriks khusus yang perlu kamu ketahui di antaranya sebagai berikut:

a. Matriks Baris

Matriks baris adalah suatu matriks yang terdiri dari satu baris aja. Contoh matriks baris:

Kalo kita lihat, matriks A, matriks P, dan matriks Q, semuanya terdiri dari satu baris dan beberapa kolom. Untuk masing-masing ordonya, berarti A_1×3, P_1×4, dan Q_1×5.

b. Matriks Kolom

Kebalikannya dari matriks baris, matriks kolom adalah suatu matriks yang terdiri dari satu kolom aja. Contoh matriks kolom:

Matriks R, matriks S, dan matriks T sama-sama terdiri dari satu kolom dan beberapa baris. Oleh karena itu, ordo matriksnya adalah R_2×1, S_3×1, dan T_4×1.

c. Matriks Persegi

Matriks persegi adalah suatu matriks yang memiliki jumlah baris dan kolom sama. Itu tandanya, m = n. Karena jumlah baris dan kolomnya sama, maka ordo matriksnya bisa kita tulis menjadi n x n, atau matriks ordo n.

Pada matriks persegi, terdapat diagonal utama, yaitu elemen-elemen matriks yang letak barisnya sama dengan letak kolomnya. Selain diagonal utama, ada juga diagonal samping atau diagonal kedua. Kalo kita tarik garis di sepanjang diagonal utama matriks, maka diagonal samping ini berada di arah sebaliknya. Contoh matriks persegi:

Nah, berdasarkan contoh di atas, matriks A memiliki jumlah baris dan kolom yang sama karena matriks ini merupakan matriks persegi, yaitu sebanyak 2. Maka, matriks ini merupakan matriks berordo 2. Kemudian, elemen-elemen pada diagonal utamanya adalah 8 dan 7. Coba deh, kalo matriks B, ordo dan diagonal utamanya apa aja, nih? Jawab di kolom komentar, ya!

d. Matriks Diagonal

Matriks diagonal adalah matriks persegi yang elemen-elemen selain diagonal utamanya bernilai nol. Contoh matriks diagonal:

Kalo kita perhatikan gambar di atas, elemen-elemen pada diagonal utama matriks Q adalah 3, 8, dan 5. Nah, di luar diagonal utama, semua elemennya bernilai 0. Misalnya, elemen Q₁₂ adalah 0, lalu elemen Q₂₁ juga 0.

e. Matriks Identitas

Matriks identitas adalah matriks persegi yang semua elemen pada diagonal utamanya bernilai satu, sedangkan elemen lainnya bernilai nol. Umumnya, matriks identitas dinotasikan dengan I disertai dengan ordonya. Contoh matriks identitas:

f. Matriks Nol

Sesuai namanya, matriks nol adalah matriks yang semua elemennya bernilai nol. Matriks nol biasanya dinotasikan dengan huruf O disertai ordonya. Contoh matriks nol:

Transpose Matriks

Oke, setelah kamu tau pengertian dan jenis-jenis matriks, kita lanjut ke materi berikutnya ya, yaitu transpose matriks.

“Bentar, bentar. Minum dulu, gan!” (sumber: giphy.com)

Apa itu transpose matriks?

Transpose matriks adalah suatu matriks yang diperoleh dari hasil pertukaran antara elemen baris dan kolomnya. Jadi, elemen-elemen pada baris akan kita tukar menjadi elemen-elemen pada kolom, atau sebaliknya. Pasti kamu bingung, kan? HAHAHAHAHA…

Yauds, kita langsung simak contoh di bawah ini, deh. Misalnya, kita akan mentranspose matriks A dan B. Maka, matriks transposenya bisa dinotasikan dengan A^t dan B^t.

Baca Juga: Cara Mencari Determinan & Invers Matriks Beserta Contohnya

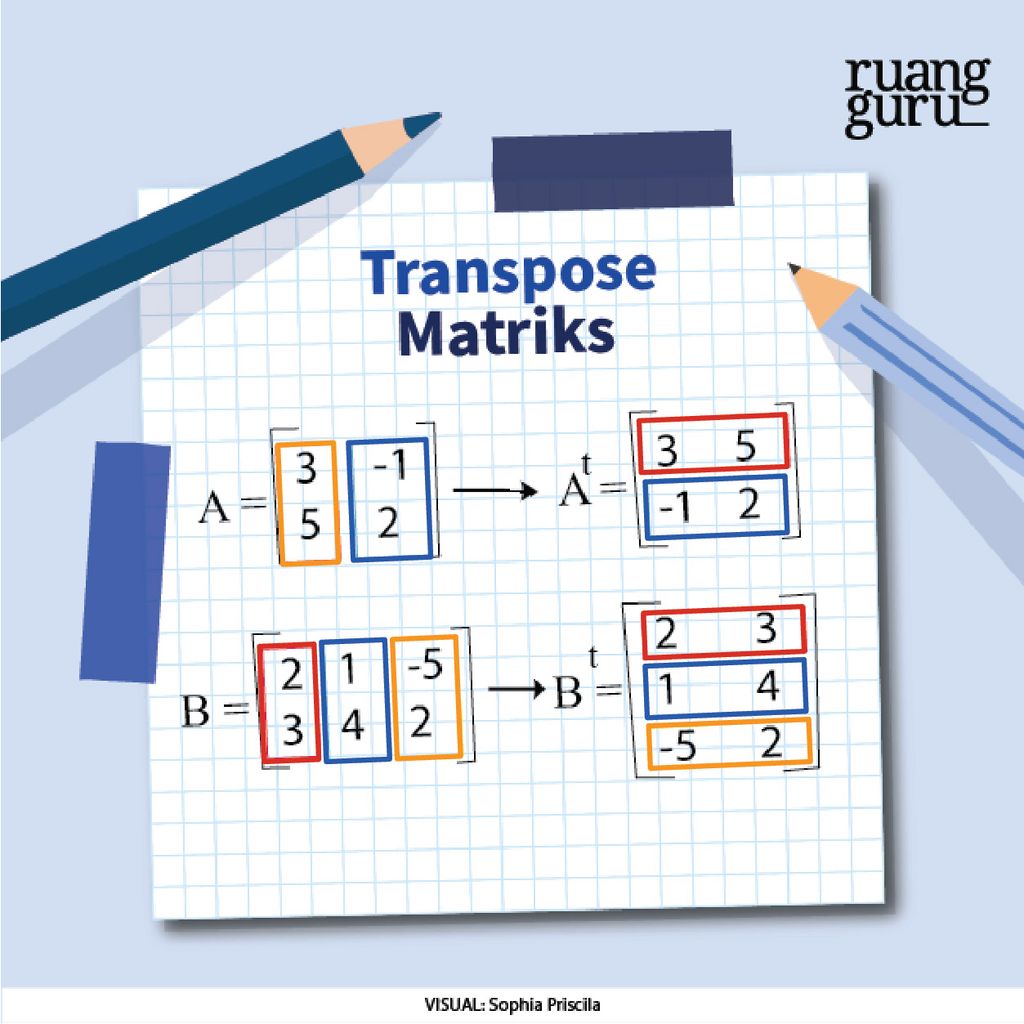
Nah, kalo kamu perhatikan kotak warna-warni pada matriks di atas, kamu pasti paham nih dengan polanya. Aku kasih contoh, ya. Coba kamu lihat matriks A dan A^t! Elemen-elemen baris ke-1 matriks A^t (yang di kotak merah), itu merupakan pertukaran dari elemen-elemen kolom ke-1 matriks A. Begitu juga dengan elemen-elemen baris ke-2 matriks A^t (yang di kotak biru), merupakan pertukaran dari elemen-elemen kolom ke-2 matriks A. Paham, ya?

Sekarang, coba kamu kerjakan contoh soal di bawah ini. Caranya sama kok kayak yang udah dijelasin sebelumnya.

Gimana, guys, udah paham dengan konsep matriks? Sebetulnya, matriks itu materi yang mudah lho, seru lagi! Matriks ini bisa digunakan untuk menyelesaikan masalah sistem persamaan yang memiliki lebih dari dua variabel dengan cepat. Dibandingkan kamu harus menggunakan metode substitusi atau eliminasi. Jadi, penting banget untuk memahami materi satu ini.

Kalo kamu merasa masih belum begitu paham dengan materi yang udah dijelaskan di artikel ini, kamu bisa coba tonton video penjelasan lengkapnya di ruangbelajar. Di sana, ada konsep kilatnya juga, lho! Membantu kamu lebih mudah memahami materi dalam waktu singkat. Yuk, buktikan sekarang!

Referensi:

Ari, R. Indriyastuti. (2012) Perspektif Matematika 3 untuk Kelas XII SMA dan MA Program Ilmu Pengetahuan Alam. PT Tiga Serangkai Pustaka Mandiri.

Sumber Foto:

Foto ‘WA Chat Pesan Nasi Goreng’ [Daring]. Tautan: https://www.suara.com/lifestyle/2021/01/06/122000/pesanan-nasi-goreng-terlalu-ribet-warganet-ini-bantu-buatkan-tabel-excel?page=all (Diakses: 7 Mei 2021)

GIF ‘Orang Minum’ [Daring]. Tautan: https://giphy.com/gifs/reaction-mood-etrntfDOQriFaBUJ7I (Diakses: 7 Mei 2021)