Statistika Deskriptif dalam Data Berinterval, Rumus, dan Contohnya | Matematika Kelas 12

Kamu sedang mempelajari statistik deskriptif dalam data berinterval? Yuk simak penjelasan rata-rata, modus, kuartil, dan simpangan baku yang akan dijelaskan dalam artikel ini!

—

Hai guys! Tahu nggak kalau Indonesia diprediksi menjadi negara dengan kekuatan ekonomi terbesar kelima di tahun 2030? Penyebab prediksi itu adalah tingginya bonus demografi di Indonesia. 

Nah, kamu tau nggak tentang apa itu bonus demografi? Jadi bonus demografi adalah suatu keadaan yang diperoleh bila proporsi penduduk berusia produktif (15 – 64 tahun) lebih banyak dari usia muda (kurang dari 15 tahun) dan usia lanjut (lebih dari 64 tahun). 

Untuk jelasnya, bisa kita lihat dari grafik yang menunjukkan interval usia populasi di Indonesia saat ini nih

Populasi Indonesia di berbagai rentang umur tahun 2017 (sumber: BPS)

Grafik di atas menunjukkan jumlah populasi penduduk Indonesia dengan interval usia tertentu. Sekilas terlihat kan penduduk usia produktif di Indonesia lebih banyak? Namun, bagaimana ya cara menunjukkannya secara kuantitatif dari statistika deskriptif? 

Pengertian Statistik Deskriptif Data Berkelompok/Interval

Dalam materi ini, kita akan mempelajari beberapa bagian, seperti rataan, modus, kuartil, dan simpangan baku. Bagian tersebut sangat dibutuhkan dalam menganalisa data. Coba deh pelajari kembali Istilah-Istilah Statistik Data Tunggal dalam Matematika untuk dapat memahami bab ini ya!

Untuk menentukan statistika deskriptif dari data berinterval, coba kamu perhatikan beberapa rumus statistika deskriptif yang sering dibutuhkan untuk data berinterval di bawah ini: 

Ukuran Pemusatan Data Interval/Kelompok

1. Rata-rata

Rata-rata adalah hasil pembagian jumlah nilai dengan banyak data. Rata-rata hitung suatu data dapat ditentukan dengan beberapa cara, yakni menggunakan nilai tengah  dan menggunakan rata-rata sementara.

2. Modus

Modus (M_O) adalah nilai data yang paling sering muncul. Letak kelas modus dapat ditentukan berdasarkan kelas yang frekuensinya paling besar. 

3. Nilai Letak Data

Nilai letak data adalah nilai yang membagi data yang berurutan menjadi beberapa bagian, diantaranya kuartil, desil, dan persentil.

Kuartil

Kuartil merupakan nilai yang membagi data yang sudah diurutkan menjadi empat bagian yang sama banyak. Kelompok data mempunyai 3 buah kuartil, yaitu Kuartil bawah (Q1), Kuartil tengah / median (Q2), dan Kuartil atas (Q3).

Desil

Desil adalah nilai yang membagi data yang sudah diurutkan menjadi sepuluh bagian yang sama banyak. Kelompok data memiliki 9 buah desil.

Persentil

Persentil adalah nilai yang membagi data yang sudah diurutkan menjadi 100 bagian yang sama banyak. Kelompok data memiliki sebanyak 99 buah persentil.

Ukuran Penyebaran Data Interval/Kelompok

1. Simpangan Rata-rata

Simpangan rata-rata atau umumnya disebut mean deviation, merupakan adalah rata-rata jarak antara nilai-nilai data menuju rata-ratanya. Kegunaan dari simpangan rata-rata ialah untuk mengetahui seberapa jauh nilai data menyimpang dari rata-ratanya.

2. Simpangan Baku (Varian dan Standar Deviasi)

Adalah ukuran-ukuran keragaman (variasi) data statistik yang paling sering digunakan. Standar deviasi (simpangan baku) merupakan akar kuadrat dari varian. Fungsi dari penghitungan simpangan baku untuk mengetahui keragaman suatu kelompok data. 

Salah satu cara untuk mengetahui keragaman dari suatu kelompok data adalah dengan mengurangi setiap nilai data dengan rata-rata kelompok data tersebut, selanjutnya semua hasilnya dijumlahkan.

Baca juga: 5 Manfaat Statistik untuk Perkembangan Indonesia

Cara Menghitung Data Interval/Berkelompok

Kalau sudah tau rumus-rumusnya, coba kita cari tau yuk salah satu statistika deskriptif dari data populasi Indonesia tahun 2017 di atas. Misalnya kita ingin menjawab

Berapa sih rata – rata umur penduduk laki-laki Indonesia dari umur 0 hingga 74 tahun?

Jika ingin mencari rata-rata, kamu butuh data jumlah banyaknya (atau biasa disebut frekuensi) tiap kelompok dan titik tengahnya. Jadi, kita harus membuat tabelnya dulu nih berdasarkan gambar grafik di atas. Tabelnya berisi kelompok umur, nilai tengah dari kelompok umur itu, frekuensi, dan hasil kali antara nilai tengah dan frekuensi.

Oh iya, tabelnya bakal kepanjangan nih jika ditampilkan semua di sini. Jadi dipersingkat ya seperti pada gambar di bawah ini (disimbolkan dengan titik-titik). Tapi tetap, kamu harus membuat tabel itu dari kelompok umur 0 – 4 tahun hingga 70 – 74 tahun ya.

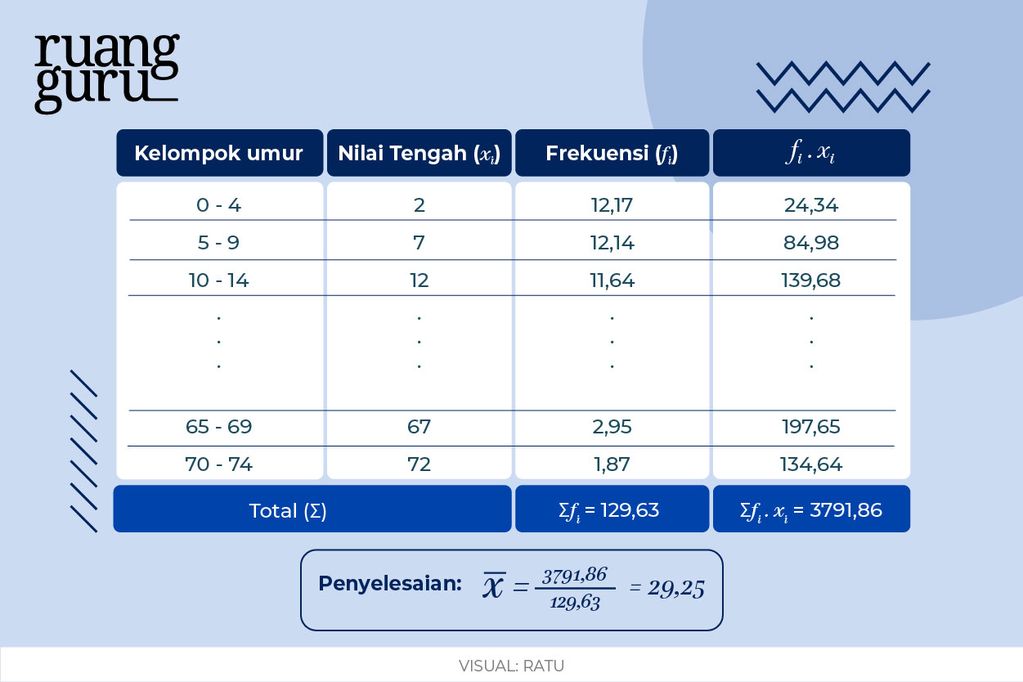
 Setelah dibuat tabelnya, didapat kan dari tabel hasil sebagai berikut:

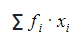= 3791,86  dan   = 129,63

Dari rumus rata-rata akan didapat

= 3791,86 / 129,63

= 29,25

Baca juga: Data Statistik Lengkap Hasil SNMPTN 2019

Jadi rata-rata umur penduduk laki-laki Indonesia dari 0 sampai 74 tahun adalah 29,25 tahun. Masih muda-muda sekali, ya!

Kalau muda kan jadi lebih produktif, punya waktu yang panjang, dan otomatis bisa membangun Indonesia lebih baik lagi. Beban penduduk usia tua juga bisa lebih terbantu nih. Apalagi kalau penduduk usia muda juga pada cerdas teknologi. Wuih bakal berjaya Indonesia. Makanya ayo belajar yang rajin ya teman-teman!

Kalau kamu butuh video materi dan pembahasan soal yang lebih banyak, langsung aja daftar di ruangbelajar. Dijamin deh jadi makin jago. Tunggu apa lagi? Yuk langsung aja langganan!