Pengertian Perbandingan, Jenis & Cara Menghitungnya | Matematika Kelas 7

Yuk, kita belajar materi perbandingan! Kita akan kupas mulai dari pengertian, jenis-jenis, cara menghitung perbandingan, hingga contoh soalnya. Baca artikel Matematika kelas 7 ini sampai habis, ya!
—
Hayo, siapa yang suka ngebanding-bandingin sesuatu?
Misalnya, ketika nilai ujian dibagikan, biasanya momen membandingkan ini selalu berlangsung. Mulai dengan penasaran dan nanya, ‘Eh, nilai lo berapa?’
Pas tahu nilai teman kita lebih besar, kita sakit hati, nyobek lembar ujian, lalu nelen bulat-bulat sambil menjerit, ‘KENAPAAAA?!!’ Masalahnya, apa, sih, pengertian perbandingan itu? Bagaimana cara membandingkan yang benar dan apa saja jenis-jenis perbandingan?

Stres karena nilai temen lebih gede saat dibandingin. (sumber: giphy.com)
Ternyata, meskipun terdengar remeh dan biasa kamu lakukan, kegiatan membandingkan itu ada kaitannya dengan matematika, lho. Ada cara-cara tertentu yang bisa kamu gunakan untuk melakukan perbandingan.
Apa yang Dimaksud dengan Perbandingan?
Dalam Matemtika, perbandingan adalah membandingkan dua nilai atau lebih dari suatu besaran yang sejenis menggunakan cara sederhana.
Misalnya nih, kita ingin membandingkan nilai a dengan b. Kita bisa menyatakannya dalam bentuk Matematika seperti di bawah ini:
a : b atau a/b
Nah, kamu pasti udah sering melihat bentuk a/b kan? Yap, bener banget! Bentuknya sama dengan bilangan pecahan. Oleh karena itu, perbandingan juga bisa dinyatakan dalam pecahan.
Baca Juga: Jenis-Jenis Bilangan Pecahan dan Contohnya
Bagaimana Cara Membandingkan Suatu Nilai?
Oke, setelah kamu mengetahui pengertian perbandingan, kita pelajari cara membandingkan, yuk! Supaya lebih mudah paham, kita langsung coba dengan soal di bawah ini, ya.
Misalnya, nilai ujian Matematika Yodi 80 dan nilai ujian matematika Rian 60. Nah, dari keterangan ini, kita dapat membandingkan data-data yang ada, yaitu:
1. Nilai ujian Yodi 20 poin lebih besar.
[Hal ini didapat dari perhitungan: 80 – 60 = 20 poin]
2. Nilai Yodi empat per tiga kali lebih besar daripada Rian.
[Hal ini didapat dari perhitungan 80/60 = 4/3]
Cara Menghitung Perbandingan
Lalu, gimana sih cara menghitung perbandingan itu? Dalam melakukan perbandingan, ada dua hal yang harus kamu perhatikan, yakni:

1. Dalam membandingkan dua besaran dengan cara menghitung hasil bagi, besaran-besaran tersebut harus merupakan besaran yang sejenis.
Contoh perbandingan yang salah:
Panjang pensil Ani ¾ kali berat badan Yudi.
Hal ini salah karena panjang pensil berada dalam satuan (cm), sementara berat badan Yudi dalam satuan kg.
Contoh perbandingan yang hampir benar:
Panjang pensil Ani 13 cm sementara panjang pensil Roberto 2 m.
Hal ini karena kedua satuannya berbeda. Sehingga, ukuran satuannya harus disamakan terlebih dahulu (menjadi sama-sama cm, atau sama-sama m).
2. Ketika melakukan perbandingan, pastikan hasil bagi kedua besaran suatu bilangan harus dalam bentuk yang paling sederhana.
Misalnya, Kakak mempunyai uang 150.000 sementara Adik 50.000. Berapa perbandingan uang mereka?
Kalau kamu menjawab 15:5 itu artinya kamu masih belum tepat. Bilangan itu masih bisa diperkecil lagi menjadi bentuk yang lebih sederhana. Berapa? Coba tulis di kolom komentar ya!
Baca Juga: Mengenal Operasi Hitung pada Pecahan
—
Sebelum kita bahas jenis-jenis perbandingan, kalo masih ada poin-poin yang belum kamu mengerti, mending belajar sama ahlinya, deh. Belajar bareng kakak-kakak pengajar di Ruangguru Privat Matematika misalnya.
Belajar nggak cuma menyenangkan, tapi kamu juga bakal diajari konsepnya sampai paham! Para pengajar di Ruangguru Privat juga sudah terstandarisasi kualitasnya, loh. Kamu juga bisa pilih nih, mau diajarkan secara langsung (offline) atau daring (online). Fleksibel, kan? Untuk info lebih lanjut, cuss klik link berikut!
Jenis-Jenis Perbandingan
Sampai sini sudah mulai paham belum? Kita lanjut, yaaa~
Perbandingan dalam Matematika dibagi menjadi dua jenis, yaitu perbandingan senilai dan perbandingan berbalik nilai. Wah, bedanya apa tuh ya? Daripada bingung, langsung simak penjelasannya, yuk!
1. Perbandingan Senilai
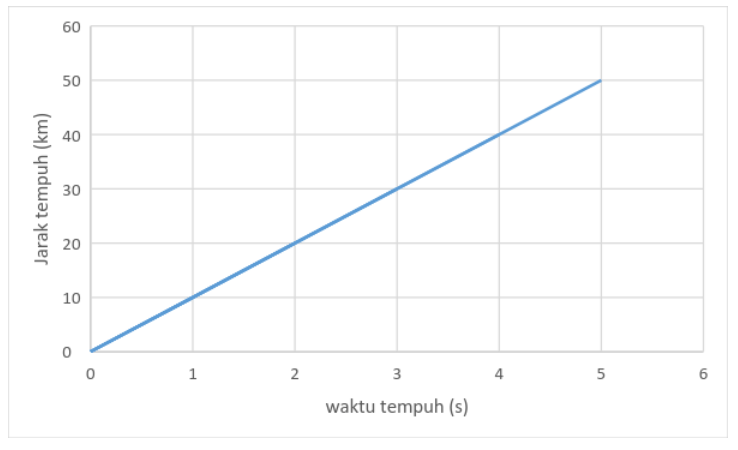
Misalnya, terdapat himpunan-himpunan bilangan A = {1, 2, 3, 4, 5} dan B = {10, 20, 30, 40, 50}.
Himpunan A menyatakan waktu tempuh dalam satuan detik dan himpunan B menyatakan jarak yang ditempuh dalam satuan kilometer. Sekarang coba, deh, kamu pikir, apa nyumabungnya antara waktu tempuh dan jarak?
Ya, betul. “sejauh”.
Kita dapat mengaitkan waktu tempuh (s) “sejauh” jarak yang dia tempuh (km). Maka hasilnya:
- 1 detik sejauh 10 km
- 2 detik sejauh 20 km
- 3 detik sejauh 30 km
- 4 detik sejauh 40 km
- 5 detik sejauh 50 km
Kalau kita buat dalam bentuk tabel, maka akan menjadi:

Kamu sudah mulai bisa melihat polanya belum? Dalam perbandingan senilai, semakin tinggi nilai yang satu (A), maka akan semakin tinggi juga nilai (B)-nya. Oleh karena itu, perbandingan jenis ini disebut sebagai perbandingan senilai. Karena nilai A akan “sejalan” dengan nilai B.
Kalau didefinisikan, perbandingan senilai adalah membandingkan dua variabel atau lebih, yang apabila nilai salah satu variabel bertambah, maka nilai variabel lainnya juga ikut bertambah.
Apabila data tadi kita olah dalam bentuk grafik koordinat kartesius, maka hasilnya akan seperti ini:
Rumus Perbandingan Senilai
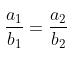
Keterangan:
a1 = variabel a sebelum dibandingkan
a2 = variabel a setelah dibandingkan
b1 = variabel b sebelum dibandingkan
b2 = variabel b setelah dibandingkan
2. Perbandingan Berbalik Nilai
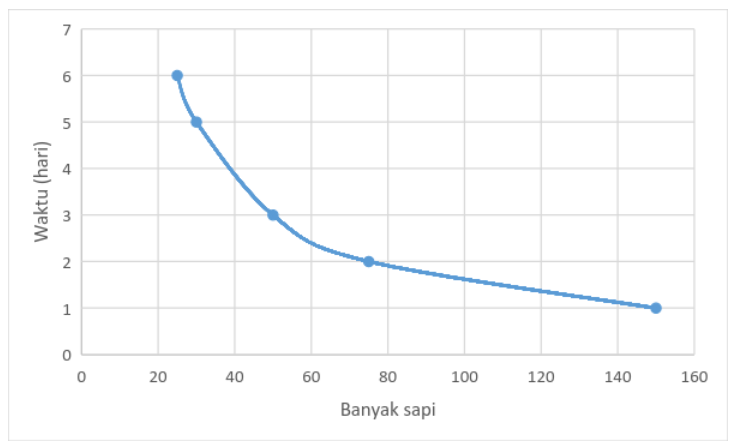
Lain halnya dengan perbandingan berbalik nilai. Misalnya, ada seorang peternak mempunyai 150 ekor sapi. Satu ikat rumput dihabiskan dalam waktu satu hari. Itu artinya, apabila peternak tersebut mempunyai
- 75 ekor sapi, pakan ternak habis dalam waktu 2 hari
- 50 ekor sapi, pakan ternak habis dalam waktu 3 hari
- 30 ekor sapi, pakan ternak dihabiskan dalam waktu 5 hari
- 25 ekor sapi, pakan ternak dihabiskan dalam waktu 6 hari
Kalau kita buat dalam bentuk tabel, maka akan terlihat seperti berikut:

Dari data itu, dapat disimpulkan bahwa semakin sedikit jumlah sapi, maka jumlah yang dibutuhkan semakin banyak. Nah, perbandingan sepert ini dinamakan dengan perbandingan berbalik nilai.
Bisa dikatakan, perbandingan berbalik nilai adalah membandingkan dua variabel atau lebih, yang apabila nilai salah satu variabel bertambah, maka nilai variabel lainnya akan berkurang, begitu juga sebaliknya.
Apabila data tadi kita olah dalam bentuk grafik koordinat akrtesius, maka hasilnya akan menjadi:
Rumus Perbandingan Berbalik Nilai
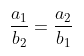
Keterangan:
a1 = variabel a sebelum dibandingkan
a2 = variabel a setelah dibandingkan
b1 = variabel b sebelum dibandingkan
b2 = variabel b setelah dibandingkan
Bagaimana, sudah mulai terlihat jelas kan perbedaan antara perbandingan senilai dan berbalik nilai. Kalau yang arahnya “sejalan”, itu termasuk ke dalam perbandingan senilai. Di sisi lain, kalau berbanding terbalik, masuk ke dalam perbandingan berbalik nilai.
Baca Juga: Penjelasan Lengkap KPK dan FPB, Apa Bedanya Ya?
3. Perbandingan Terkait Jumlah dan Selisih
Nah, selain perbandingan senilai dan berbalik nilai, ada juga perbandingan terkait jumlah dan selisih. Jenis perbandingan ini sedikit kompleks, tapi sebenarnya mudah dipahami. Kita bahas satu per satu secara perlahan ya.
a. Perbandingan Berdasarkan Jumlah
Perbandingan berdasarkan jumlah digunakan ketika soal yang diketahui adalah total keseluruhan dari dua nilai atau lebih. Biasanya, dalam soal terdapat kata kunci seperti jumlah, total, atau keseluruhan. Supaya kamu lebih paham, kita langsung masuk ke contoh soalnya, deh.
Misalnya, Fany dan Fahri mempunyai permen dengan jumlah 40 buah. Perbandingan permen Fany dan Fahri adalah 1 : 3. Berapa jumlah masing-masing permen Fany dan Fahri?
Untuk menjawab soal di atas, kita bisa menggunakan rumus perbandingan berdasarkan jumlah seperti di bawah ini:
Rumus Perbandingan berdasarkan Jumlah

Sehingga, penyelesaiannya bisa kita cari dengan:
Diketahui:
Jumlah permen Fany dan Fahri = 40
Perbandingan permen Fany dan Fahri = 1 : 3
Jumlah perbandingan = 1 + 3 = 4
Ditanya:
a. Jumlah permen Fany?
b. Jumlah permen Fahri?
Penyelesaian:

Jadi, jumlah permen Fany adalah 10 dan jumlah permen Fahri adalah 30.
b. Perbandingan Berdasarkan Selisih
Nah, kebalikannya, perbandingan berdasarkan selisih digunakan ketika soal yang diketahui adalah selisih dari dua nilai atau lebih. Biasanya, dalam soal terdapat kata kunci seperti selisih, lebih banyak, atau lebih tua. Kita perhatikan contoh soal di bawah ini, ya.
Perbandingan umur kakak dan adik adalah 7 : 5. Jika selisih umur mereka 4 tahun, tentukan umur kakak dan adik.
Soal di atas bisa kita selesaikan menggunakan rumus perbandingan berdasarkan selisih seperti di bawah ini:
Rumus Perbandingan berdasarkan Selisih

Sehingga, penyelesaiannya bisa kita cari dengan:
Diketahui:
Selisih umur kakak dan adik = 4 tahun
Perbandingan umur kakak dan adik = 7 : 5
Selisih perbandingan = 7 – 5 = 2
Ditanya:
a. Berapa umur kakak?
b. Berapa umur adik?
Penyelesaian:

Jadi, umur kakak adalah 14 tahun dan umur adik adalah 10 tahun.
Contoh Soal Perbandingan
1. Sebuah mobil membutuhkan 4 liter bensin untuk perjalanan sejauh 72 km. Berapa bensin yang dibutuhkan jika mobil itu akan menempuh perjalanan 54 km?
- 1 liter
- 1,5 liter
- 3 liter
- 3,5 liter
Pembahasan:
Diketahui:
4 liter = 72 km
x liter = 54 km
Soal ini bisa kita selesaikan menggunakan rumus perbandingan senilai:
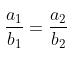

Sehingga, diketahui bahwa, mobil tersebut membutuhkan 3 liter bensin agar dapat menempuh perjalanan sejauh 54 km.
2. Proyek perbaikan jalan akan selesai selama 30 hari dengan pekerja sebanyak 15 orang. Setelah 6 hari pelaksanaan, proyek tersebut dihentikan selama 4 hari karena suatu hal. Jika kemampuan bekerja setiap orang sama, agar proyek tersebut selesai tepat waktu, pekerja tambahan yang diperlukan adalah …
- 1 orang
- 3 orang
- 6 orang
- 9 orang
Pembahasan:
Diketahui:
30 hari —> 15 pekerja
setelah 6 hari: 24 hari —> 15 pekerja
dihentikan 4 hari: 20 hari —> 15 pekerja + tambahan pekerja
Ditanya: tambahan pekerja …?
Jawab:
Jika data-data di atas dibuat dalam bentuk tabel, maka:
| Waktu | Pekerja |
| 30 | 15 |
| 24 | 15 |
| 20 | x |
Nah, untuk soal ini, kita bisa menyelesaikannya dengan rumus perbandingan berbalik nilai.
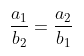
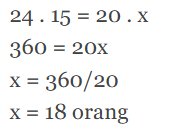
Eiits, jangan keliru ya! Karena yang diminta pada soal adalah tambahan pekerja, maka jawaban di atas belum selesai, nih.
Tambahan pekerja = x – 15 orang pekerja
Tambahan pekerja = 18 – 15 = 3 orang
Sehingga, dibutuhkan 3 orang tambahan pekerja agar proyek tersebut dapat selesai tepat waktu.
—
Gimana, gais? Semoga pembahasan mengenai pengertian dan jenis-jenis perbandingan ini bisa kamu pahami dengan baik, ya. Kalau kamu masih ada kesulitan atau tambahan, jangan ragu untuk tulis di kolom komentar. Lebih suka memelajari materi seperti ini sambil menonton video animasi lucu? ruangbelajar jawabannya!
Referensi:
Raharjo M. (2018) Matematika SMP/MTs Kelas VII. Jakarta: Erlangga
Sumber foto:
GIF ‘Orang Menangis’ [Daring]. Tautan: https://giphy.com/gifs/teamcoco-crying-cry-l2JhtKtDWYNKdRpoA (Diakses: 22 Desember 2020)

















