Rumus Luas & Volume Kerucut serta Contoh Soalnya | Matematika Kelas 9

Ternyata bentuk cone ice cream itu mirip dengan kerucut. Kok bisa? Terus gimana sih caranya menghitung luas dan volume kerucut? Yuk simak selengkapnya di artikel pelajaran Matematika kelas 9 ini!

—

Siapa di antara kamu yang suka ice cream?

Rata-rata dari kamu pasti udah familiar banget kan sama makanan yang satu ini. Biasanya kalo kita beli ice cream ada 2 pilihan, pakai cup atau cone.

Kamu termasuk tim yang mana nih, cup atau cone?

Hmm kalo aku sih prefer cone karena bisa dimakan habis semuanya hehehe…

By the way, kamu tahu nggak awal mula cone ice cream itu dari mana? Nih aku ceritain!

Jadi ada penjual waffle namanya Ernest Hamwi, dia gulung waffle kering buatannya sampai berbentuk kerucut. Setelah itu, diberikan ke penjual ice cream untuk taruh ice cream di atas cone atau kerucut tersebut. Ide Hamwi ini berhasil loh karena banyak pelanggan yang menyukainya.

Nah, cone itu berbentuk kerucut! ngomongin tentang kerucut nih, banyak juga loh benda-benda di sekitar kita yang juga berbentuk kerucut. Misal topi petani atau topi ulang tahun, nasi tumpeng, sampai pembatas jalan (traffic cone) dan masih banyak lagi.

Bisa dibilang kerucut ini berkaitan erat banget ya sama kehidupan kita. Sekarang, yuk kita cari tahu lebih lagi tentang kerucut!

Pengertian dan Bagian-Bagian Kerucut

Kerucut itu termasuk bangun ruang ya! karena berbentuk tiga dimensi, memiliki sisi melengkung sebagai selimut dan alasnya berbentuk lingkaran. Bisa dikatakan bahwa kerucut adalah limas dengan alas berbentuk lingkaran.

Baca Juga: Rumus Luas dan Volume Limas serta Contoh Soalnya

Unsur dan Sifat-Sifat Kerucut

Nah, kerucut dan tabung itu ada kemiripan loh, sama-sama memiliki alas berbentuk lingkaran. Yuk, cek ciri-ciri tabung di sini dulu kalau kamu lupa!

Perbedaan antara kerucut dan tabung terdapat pada selimutnya. Selimut kerucut maksudnya adalah sisi tegak kerucut. Kalau kamu masih bingung letak dari sisi, rusuk, dan bagian kerucut lainnya, liat ini dulu dehh!

Udah tahu, kan, apa aja bagian dan sifat-sifat dari kerucut. Nah, jadi tinggi kerucut maksudnya jarak dari puncak ke alas kerucut. Sedangkan untuk garis pelukis atau apotema adalah garis yang menghubungkan titik puncak sama titik keliling alas. Nah, r, s, dan t berhubungan dan membentuk persamaan pythagoras kayak gini:

Dari jaring-jaring kerucut yang udah dibahas sebelumnya, kita bisa menentukan rumus luas permukaan dan volume kerucut. Ktia coba bahas satu per satu ya!

Baca Juga: Cara Menghitung Luas dan Volume Bola

Cara Menghitung Luas Permukaan Kerucut

Untuk luas permukaan kerucut, kita bisa jumlahkan luas semua bangun yang menyusun kerucutnya. Bangun apa aja sih yang dimaksud? Yaa, betul banget! ada juring dan lingkaran. Pokoknya nggak boleh lupa sama kedua bangun ini.

Rumus Mencari Luas Permukaan Kerucut

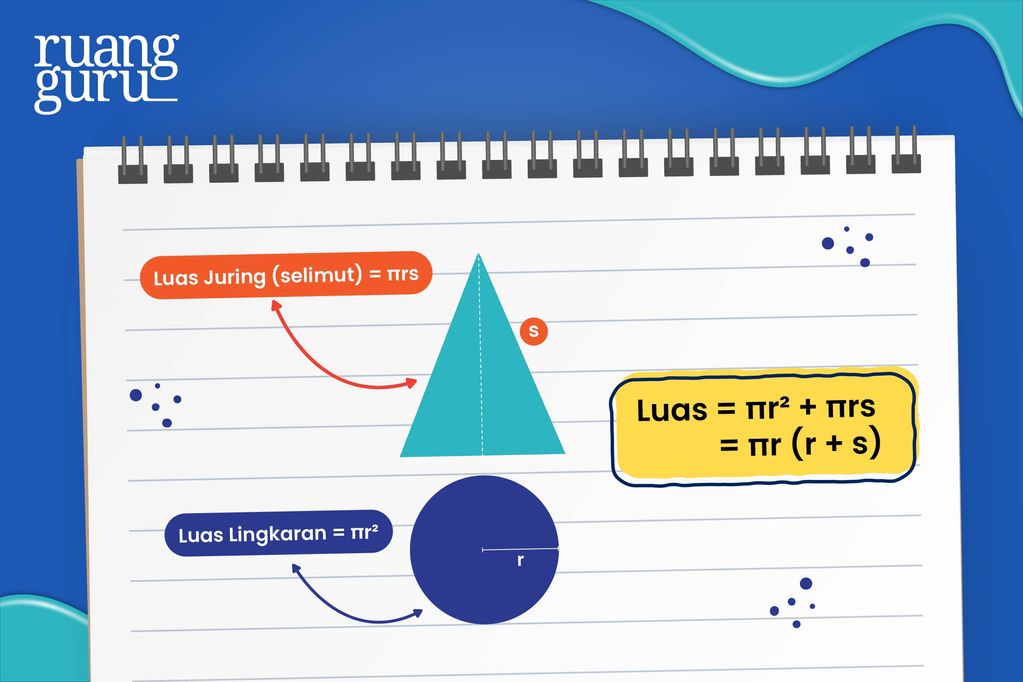
Jangan lupa juga nilai π = 3,14 atau 22/7, r = jari-jari alas kerucut, dan s = garis pelukis kerucut.

Kalau misalnya kamu udah lupa banget sama rumus luas permukaan kerucut, yaudah kamu bisa bayangin kerucut yang diiris tegak salah 1 bagiannya dari puncak sampai alas, inget ya diiris tegak bukan melintang.

Nah, nanti tinggal dijumlahkan luas dari kedua bangun itu, jadi lebih gampang kan ingetnya?

Contoh Soal Luas Permukaan Kerucut

Hitunglah berapa luas permukaan kerucut yang mempunyai diameter 14 cm dan garis pelukis 15 cm!

Pembahasan:

Diketahui:

• diameter kerucut (d) = 14 cm, berarti jari-jari kerucut adalah setengah dari diameternya, yaitu r = 7 cm.
• garis pelukis (s) = 15 cm

Ditanya: luas permukaan kerucut …?

Jawab:

Luas permukaan kerucut = π · r (r + s)

Luas permukaan kerucut = (22/7) · 7 (7 + 15)      (sederhanakan angka yang warnanya sama)

Luas permukaan kerucut = 22 × 22  = 484 cm²

Jadi, luas permukaan kerucut tersebut adalah 484 cm².

Cara Menghitung Volume Kerucut

Kamu harus tau nih, kalo volume kerucut itu ⅓ bagian dari volume tabung. Jadi kalo kita ambil ⅓ bagian dari volume tabung, kita bakal dapat rumus volume kerucutnya.

“Masih ingat nggak rumus volume tabung?”

“Emm volume tabung itu phi r kuadrat dikali tinggi.”

Berarti rumus volume kerucutnya gimana dong? Langsung liat ini aja yuk!

Rumus Mencari Volume Kerucut

Perlu diingat, satuan volume kerucut adalah kubik dengan lambang pangkat 3. Misalnya, sentimeter kubik (cm³) dan meter kubik (m³).

Contoh Soal Volume Kerucut

1. Diketahui jari-jari alas kerucut adalah 7 cm. Jika tinggi kerucut adalah 6 cm, berapakah volume kerucut tersebut?

Pembahasan:

Diketahui: r = 7 cm, t = 6 cm

Ditanya: volume kerucut …?

Jawab:

Volume kerucut = 1/3 · π · r² · t

Volume kerucut = 1/3 · 22/7 · (7)² · 6       (sederhanakan angka-angka yang warnanya sama)

Volume kerucut = 1 · 22 · 7 · 2

Volume kerucut = 308 cm³

Jadi, volume kerucut tersebut adalah 308 cm³.

Baca Juga: Cara Menghitung Luas Permukaan dan Volume Gabungan Bangun Ruang Sisi Lengkung

Okey, udah banyak banget pembahasan kita kali ini. Mulai dari sifat, unsur sampai rumus-rumus kerucut. Sekarang aku akan bahas satu soal tapi untuk soal kedua, aku mau tantang kalian untuk menyelesaikan sendiri ya!

Gimana nih, bisa nggak nyelesain volume kerucutnya?

Nah, kalo kamu masih mau bahas soal dan kenalan sama bangun ruang sisi lengkung lainnya, langsung aja ke ruangbelajar! Banyak soal-soal terupdate, lengkap dengan pembahasannya yang bikin pemahaman konsep kamu meningkat. Kalo pemahaman kamu udah oke, pasti soal-soal HOTS dengan variasi apapun bisa kamu selesaikan deh, so tunggu apalagi!

Referensi:

Subchan, dkk. (2018) Matematika SMP/MTs Kelas IX. Jakarta: Pusat Perbukuan, Departemen Pendidikan Nasional.

Indarsih. (2009) Mempelajari Bangun Ruang Kerucut. Klaten: PT Intan Pariwara