Rangkuman Materi Matematika Kelas 10 Kurikulum Merdeka

Yuk, cek daftar lengkap materi pelajaran Matematika kelas 10 SMA, mulai dari semester 1 hingga semester 2, sesuai Kurikulum Merdeka!
—
Matematika sering jadi mata pelajaran yang bikin banyak siswa merasa pusing. Padahal, kalau sudah tau cara belajar yang tepat dan memahami konsep dasarnya, Matematika justru bisa terasa seru dan menantang, lho. Nah, di kelas 10 SMA ini, kamu akan mulai mempelajari berbagai materi penting yang menjadi fondasi untuk pelajaran di tingkat berikutnya.
Supaya kamu lebih siap belajarnya, kita akan membahas materi Matematika kelas 10 SMA untuk semester 1 dan 2 berdasarkan Kurikulum Merdeka. Kakak juga bakal spill alasan kenapa materi ini penting dipahami dan tips belajar supaya lebih mudah mengerti Matematika. Yuk, simak!
Materi Pelajaran Matematika Kelas 10 Semester 1 Kurikulum Merdeka
Kita mulai dulu dari daftar materi Matematika kelas 10 Semester 1, ya. Fokus pembelajaran di semester ini, kamu akan memahami konsep bilangan berpangkat (eksponen), logaritma, barisan dan deret, vektor, dan trigonometri, dengan cakupan yang lebih kompleks lagi dibanding SMP. Simak selengkapnya di bawah ini!
Bab I – Eksponen dan Logaritma
| Topik | Subtopik | Ringkasan |
| Eksponen | Definisi Eksponen | Eksponen merupakan bentuk penulisan perkalian berulang dari suatu bilangan yang disebut sebagai bilangan pokok. Konsep ini digunakan untuk menyederhanakan penulisan bilangan yang sangat besar atau sangat kecil. Dalam pembelajaran Matematika, eksponen menjadi dasar untuk memahami berbagai konsep lanjutan seperti bentuk akar, logaritma, dan fungsi eksponensial. |
| Sifat-Sifat Eksponen | Terdapat beberapa sifat penting eksponen, seperti perkalian dan pembagian dengan basis yang sama, pangkat dari suatu pangkat, serta pangkat nol dan negatif. Pemahaman sifat-sifat eksponen ini, membantu dalam menyederhanakan bentuk aljabar dan menyelesaikan perhitungan dengan lebih efisien dan sistematis. | |
| Fungsi Eksponen | Fungsi eksponen adalah fungsi matematika yang melibatkan variabel sebagai pangkat. Fungsi ini sering digunakan untuk memodelkan peristiwa pertumbuhan dan peluruhan dalam kehidupan sehari-hari, seperti pertumbuhan populasi, penyebaran virus, dan peluruhan zat radioaktif.
|
|
| Bentuk Akar | Bentuk akar merupakan bentuk lain dari bilangan berpangkat pecahan. Materi ini penting karena sering muncul dalam penyederhanaan aljabar dan penyelesaian persamaan matematika. Pemahaman bentuk akar membantu dalam menghubungkan konsep eksponen dengan bentuk matematika lainnya.
|
|
| Logaritma | Definisi Logaritma |
Logaritma merupakan kebalikan dari operasi eksponen. Jika suatu bilangan berpangkat menghasilkan nilai tertentu, maka logaritma digunakan untuk mencari pangkat tersebut. Misalnya, jika ax = b , maka alog b = x. Konsep logaritma membantu dalam menyelesaikan persoalan eksponensial dengan cara yang lebih sederhana dan terstruktur. |
| Sifat-Sifat Logaritma | Sifat-sifat logaritma seperti logaritma dari perkalian, pembagian, dan pangkat, sangat berguna untuk menyederhanakan perhitungan. Pemahaman sifat-sifat ini memudahkan dalam menyelesaikan soal yang lebih kompleks. |
Baca Juga: Bentuk-Bentuk Persamaan Logaritma dan Cara Menyelesaikannya
Bab II – Barisan dan Deret
| Topik | Subtopik | Ringkasan |
| Barisan | Barisan Aritmatika | Barisan aritmatika adalah barisan bilangan yang memiliki selisih tetap antara satu suku dengan suku berikutnya. Selisih ini disebut beda (b). Contohnya adalah 2, 4, 6, 8,… dengan selisih 2. Melalui barisan aritmatika, kamu dapat belajar mengenali pola bilangan yang bertambah atau berkurang secara teratur, serta menentukan suku ke-n berdasarkan pola tersebut. |
| Barisan Geometri | Barisan geometri merupakan barisan bilangan yang memiliki rasio tetap antara dua suku yang berurutan (r). Rasio ini diperoleh dengan membagi suatu suku dengan suku sebelumnya. Misalnya, 3, 6, 12, 24,… memiliki rasio 2. Konsep barisan geometri membantu kamu dalam memahami pola pertumbuhan yang berlipat ganda atau menyusut secara teratur. | |
| Deret | Deret Aritmatika | Deret aritmatika merupakan penjumlahan dari barisan aritmatika. Rumus jumlahnya yaitu 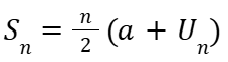 . Deret aritmatika sering digunakan untuk menyelesaikan masalah sehari-hari yang berkaitan dengan penjumlahan bertahap. . Deret aritmatika sering digunakan untuk menyelesaikan masalah sehari-hari yang berkaitan dengan penjumlahan bertahap. |
| Deret Geometri | Deret geometri merupakan penjumlahan suku-suku dari barisan geometri. Nilai deret ini bergantung pada rasio yang digunakan. Jika rasio r < 1, maka deret bisa konvergen. Pemahaman deret geometri membantu kamu dalam menganalisis pola pertumbuhan atau penurunan yang bersifat eksponensial dalam berbagai situasi. | |
| Deret Geometri Tak Hingga | Deret geometri tak hingga adalah deret geometri yang jumlah sukunya tidak terbatas. Meskipun jumlah sukunya tak hingga, deret ini dapat memiliki nilai tertentu jika nilai mutlak rasionya kurang dari satu. Jumlahnya dapat dihitung menggunakan rumus 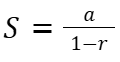 jika |r| < 1 . jika |r| < 1 . |
Baca Juga: Barisan Aritmatika Bertingkat: Konsep Dasar, Rumus & Contoh Soal
Bab III – Vektor dan Operasinya
| Topik | Subtopik | Ringkasan |
| Terminologi, Notasi, dan Jenis Vektor | Panjang dan Arah Vektor | Setiap vektor memiliki panjang (besar) dan arah. Panjang vektor menunjukkan seberapa besar nilai vektor tersebut, sedangkan arah vektor menunjukkan orientasinya dalam ruang. Dua vektor dapat memiliki panjang yang sama, tetapi jika arahnya berbeda, maka keduanya tidak dianggap sebagai vektor yang sama. |
| Vektor Negatif atau Vektor Lawan | Vektor negatif adalah vektor yang memiliki panjang yang sama dengan vektor asal, tetapi arahnya berlawanan. Vektor ini diperoleh dengan mengalikan vektor dengan bilangan negatif. Dalam operasi vektor, vektor negatif sering digunakan untuk mempermudah proses pengurangan vektor. | |
| Vektor Ekuivalen (Vektor yang Sama) | Dua vektor dikatakan ekuivalen jika memiliki panjang dan arah yang sama, meskipun letaknya berbeda. Artinya, posisi awal vektor tidak memengaruhi kesetaraannya. Konsep ini penting karena vektor lebih menekankan besar dan arah, bukan titik pangkalnya. | |
| Vektor dalam Sistem Koordinat | Vektor Berdimensi Dua pada Sistem Koordinat | Vektor berdimensi dua merupakan vektor yang terletak pada bidang datar dengan dua sumbu, yaitu sumbu x dan sumbu y. Vektor ini biasanya dinyatakan dalam bentuk pasangan bilangan yang menunjukkan perpindahan secara horizontal dan vertikal. |
| Komponen-Komponen Vektor | Setiap vektor dapat diuraikan menjadi komponen-komponen berdasarkan arah sumbu koordinat. Komponen vektor menunjukkan kontribusi vektor pada masing-masing sumbu. Dengan menggunakan komponen ini, perhitungan vektor dapat dilakukan dengan lebih mudah dan sistematis. | |
| Vektor-Vektor Ekuivalen pada Sistem Koordinat Kartesius | Dalam sistem koordinat Kartesius, dua vektor dianggap ekuivalen jika memiliki komponen, panjang, dan arah yang sama, meskipun titik awalnya berbeda. Hal ini menunjukkan bahwa vektor dapat dipindahkan secara sejajar tanpa mengubah nilainya. | |
| Vektor Berdimensi Tiga pada Sistem Koordinat Kartesius | Vektor berdimensi tiga berada dalam ruang tiga dimensi dengan sumbu x, y, dan z. Vektor ini digunakan untuk menggambarkan posisi dan arah dalam ruang, misalnya pada bidang fisika, teknik, dan geometri ruang. | |
| Vektor Kolom dan Vektor Baris | Vektor dapat dituliskan dalam bentuk matriks satu kolom (vektor kolom) atau satu baris (vektor baris). Bentuk penulisan ini sangat penting dalam operasi matriks dan perhitungan aljabar linear. | |
| Vektor Satuan dari Suatu Vektor | Vektor satuan adalah vektor yang memiliki panjang satu satuan dan menunjukkan suatu arah tertentu. Vektor ini diperoleh dengan membagi vektor asal dengan panjangnya. Vektor satuan digunakan untuk menyatakan arah tanpa memperhatikan besarannya. | |
| Vektor Posisi | Vektor posisi adalah vektor yang menunjukkan letak suatu titik terhadap titik acuan, biasanya titik asal koordinat. Vektor ini menggambarkan perpindahan dari titik (0,0) atau (0,0,0) menuju suatu titik tertentu dalam ruang. | |
| Vektor Berkebalikan | Vektor berkebalikan merupakan vektor yang memiliki besar yang sama dengan vektor asal, tetapi arahnya berlawanan. Vektor ini sering digunakan dalam analisis gerak dan perhitungan resultan gaya. | |
| Operasi Vektor | Penjumlahan Vektor | Penjumlahan vektor dapat dilakukan dengan beberapa metode, seperti metode segitiga, jajar genjang, dan poligon, atau dengan menjumlahkan komponen-komponennya. Hasil dari penjumlahan ini, disebut vektor resultan yang menunjukkan pengaruh gabungan dari beberapa vektor. |
| Pengurangan Vektor | Pengurangan vektor dilakukan dengan menambahkan vektor negatif dari vektor yang dikurangkan. Dengan cara ini, pengurangan vektor dapat diubah menjadi operasi penjumlahan, sehingga lebih mudah untuk dihitung. | |
| Perkalian Skalar dengan Vektor | Perkalian skalar dengan vektor menghasilkan vektor baru yang besarnya berubah sesuai nilai skalar. Jika skalar bernilai positif, arah vektor tetap, sedangkan jika bernilai negatif, arah vektor akan berlawanan. Operasi ini digunakan untuk memperbesar, memperkecil, atau membalik arah vektor. |
Bab IV – Trigonometri
| Topik | Subtopik | Ringkasan |
| Perbandingan Trigonometri | Penamaan Sisi Segitiga Siku-Siku | Dalam segitiga siku-siku, setiap sisi memiliki nama berdasarkan letaknya terhadap sudut yang diamati, yaitu sisi depan, sisi samping, dan sisi miring. Memahami penamaan sisi ini sangat penting agar kamu dapat menggunakan rumus trigonometri dengan tepat. |
| Satu Jenis Perbandingan Trigonometri tan θ | Perbandingan tan θ menyatakan hubungan antara panjang sisi depan dan sisi samping pada segitiga siku-siku. Konsep ini digunakan untuk membantu menentukan nilai sudut, tinggi, atau jarak suatu objek. | |
| Kegunaan Perbandingan Trigonometri tan θ |
Nilai tan θ sering dimanfaatkan untuk menghitung tinggi benda, seperti gedung, menara, atau pohon tanpa perlu mengukurnya secara langsung. Selain itu, perbandingan ini juga banyak digunakan dalam bidang navigasi, teknik, dan konstruksi. | |
| Pemanfaatan Perbandingan Trigonometri | Perbandingan Trigonometri di Piramida | Penerapan trigonometri sudah digunakan sejak zaman dahulu, salah satunya dalam mengukur tinggi piramida. Hal ini menunjukkan bahwa konsep trigonometri memiliki peran penting dalam perkembangan ilmu pengetahuan dan arsitektur. |
| Tiga Serangkai Perbandingan Trigonometri | Dalam trigonometri, terdapat tiga perbandingan utama, yaitu sinus (sin), cosinus (cos), dan tangen (tan). Ketiga perbandingan ini sering digunakan untuk menyelesaikan berbagai permasalahan dalam Matematika, Sains, dan kehidupan sehari-hari. | |
| Sudut Istimewa Perbandingan Trigonometri | Sudut-sudut tertentu seperti 30°, 45°, dan 60° memiliki nilai perbandingan trigonometri yang khusus. Dengan menghafal dan memahami nilai-nilai ini, kamu dapat mengerjakan soal trigonometri dengan lebih cepat dan mudah. |
—
Sebelum kita bahas materi Matematika Semester 2, kalo masih ada poin-poin yang belum kamu mengerti, mending belajar sama ahlinya, deh. Belajar bareng kakak-kakak pengajar di Ruangguru Privat Matematika misalnya.
Belajar nggak cuma menyenangkan, tapi kamu juga bakal diajari konsepnya sampai paham! Para pengajar di Ruangguru Privat juga sudah terstandarisasi kualitasnya, loh. Kamu juga bisa pilih nih, mau diajarkan secara langsung (offline) atau daring (online). Fleksibel, kan? Untuk info lebih lanjut, cuss klik link berikut!
Materi Pelajaran Matematika Kelas 10 Semester 2 Kurikulum Merdeka
Next, kita lanjut ke daftar materi Matematika kelas 10 Semester 2. Pada semester ini, kamu akan dilatih untuk menganalisis data dalam topik statistika, memahami bentuk grafik dan persamaan fungsi kuadrat, sistem persamaan dan pertidaksamaan linear, serta mencari tau probabilitas sebuah kejadian dalam peluang. Berikut topik dan subtopik yang bakal kamu pelajari!
Bab V – Sistem Persamaan dan Pertidaksamaan Linear
| Topik | Subtopik | Ringkasan |
| Sistem Persamaan dan Pertidaksamaan Linear | Sistem Persamaan Linear | Sistem persamaan linear terdiri dari dua atau lebih persamaan yang diselesaikan secara bersamaan. Tujuan utamanya untuk menentukan nilai variabel yang memenuhi semua persamaan tersebut secara bersamaan. |
| Sistem Pertidaksamaan Linear | Sistem pertidaksamaan linear menyatakan hubungan yang tidak sama, seperti lebih besar atau lebih kecil dari suatu nilai. Materi ini digunakan untuk menentukan batasan solusi dalam berbagai permasalahan matematika maupun situasi kehidupan sehari-hari. |
Bab VI – Fungsi Kuadrat
| Topik | Subtopik | Ringkasan |
| Fungsi Kuadrat | Karakteristik Fungsi Kuadrat | Fungsi kuadrat memiliki berbentuk umum y = ax2 + bx + c dengan grafik berupa parabola. Kamu juga perlu memahami ciri-ciri pentingnya, seperti titik puncak, sumbu simetri, dan arah buka parabola. |
| Mengkonstruksi Fungsi Kuadrat | Fungsi kuadrat dapat dibentuk dari grafik, tabel, atau data yang diketahui. Proses ini membantu memahami hubungan antara bentuk aljabar dengan representasi visualnya. | |
| Menyelesaikan Masalah dengan Fungsi Kuadrat | Fungsi kuadrat banyak digunakan untuk menyelesaikan masalah praktis, seperti menentukan waktu atau tinggi maksimum. Materi ini sering muncul dalam soal-soal HOTS dan aplikasi sehari-hari. |
Bab VII – Statistika
| Topik | Subtopik | Ringkasan |
| Statistika | Histogram | Histogram adalah diagram batang yang digunakan untuk menampilkan distribusi frekuensi data. Grafik ini membantu melihat pola, kecenderungan, dan sebaran data secara visual. |
| Frekuensi Relatif | Frekuensi relatif menunjukkan perbandingan jumlah kemunculan suatu data terhadap keseluruhan data. Konsep ini digunakan untuk mengetahui proporsi setiap nilai dalam suatu kumpulan data. | |
| Ukuran Pemusatan Data |
|
|
| Ukuran Penempatan (Measure of Location) |
|
|
| Ukuran Penyebaran |
|
Baca Juga: Statistika Deskriptif dalam Data Berinterval, Rumus & Contohnya
Bab VIII – Peluang
| Topik | Subtopik | Ringkasan |
| Peluang | Distribusi Peluang | Distribusi peluang menunjukkan semua kemungkinan hasil dari suatu percobaan beserta peluang terjadinya. Konsep ini menjadi dasar dalam mempelajari probabilitas dalam Matematika dan Statistika. |
| Aturan Penjumlahan |
|
Baca Juga: Pengertian Titik Sampel, Ruang Sampel & Percobaan dalam Peluang
Pentingnya Memahami Materi Pelajaran Matematika SMA
Jujur aja, pasti banyak dari kamu yang mikir kalau Matematika itu pelajaran paling ribet dan bikin pusing. Rumusnya banyak, hitungannya panjang, dan kadang bikin stres. Tapi sebenarnya, kalau dipahami pelan-pelan, Matematika itu punya manfaat besar banget buat kita, lho.
Pertama, Matematika bikin kita terbiasa berpikir logis dan teratur. Setiap mengerjakan soal, kita dilatih buat mikir langkah demi langkah sampai menemukan jawabannya. Kebiasaan ini berguna juga di kehidupan sehari-hari, misalnya waktu kita mengatur waktu, menyusun rencana, atau menyelesaikan masalah.
Kedua, hampir semua pelajaran lain itu butuh Matematika. Contohnya, Fisika, Kimia, Biologi, Ekonomi, Sosiologi, bahkan Teknologi dan Komputer juga nggak lepas dari hitung-hitungan. Kalau dasar Matematika kita kuat, belajar mapel lain juga jadi lebih gampang dan nggak terlalu bikin pusing.
Ketiga, buat kamu yang punya cita-cita masuk jurusan keren kayak Teknik, Ilmu Komputer, Ekonomi, atau jurusan sains lainnya, Matematika itu wajib banget dikuasai. Soalnya, di jurusan-jurusan itu, kamu bakal sering ketemu angka, rumus, dan analisis data.
Selain itu, belajar Matematika juga bisa bikin kita jadi lebih sabar dan teliti. Mengerjakan soal yang susah memang bikin emosi, tapi pas akhirnya berhasil nemu jawabannya, rasanya puas banget. Dari situ, rasa percaya diri kita juga ikut naik.
Jadi, sebenarnya belajar Matematika itu bukan cuma soal dapet nilai bagus, tapi juga soal melatih cara berpikir dan menyiapkan diri di masa depan. Kalau kita bisa pelan-pelan berdamai dengan Matematika, pelajaran ini bisa jadi bekal penting buat hidup kita nanti.
Baca Juga: Cara Mudah Belajar Matematika biar Cepat Paham!
Tips Efektif Belajar Matematika
Dengan menerapkan strategi yang tepat, kamu bisa memahami materi dengan lebih mudah. Yuk, coba terapkan beberapa tips berikut biar belajar Matematika makin lancar:
1. Pahami Konsep Dasar, Bukan Sekadar Menghafal Rumus
Jangan langsung fokus menghafal rumus tanpa memahami maknanya. Cobalah pahami terlebih dahulu mengapa rumus tersebut digunakan dan bagaimana cara kerjanya. Dengan memahami konsep dasar, kamu akan lebih mudah mengingat rumus dan menggunakannya dalam berbagai jenis soal.
2. Perbanyak Latihan Soal Secara Rutin
Semakin sering kamu berlatih, semakin terbiasa kamu menghadapi berbagai bentuk soal. Nggak harus langsung banyak, kok. Sedikit tapi rutin jauh lebih efektif daripada belajar kebut semalam sebelum ujian. Mulailah dari soal yang mudah, lalu tingkatkan ke soal yang lebih menantang.
3. Manfaatkan Sumber Belajar Visual
Kalau baca buku bikin ngantuk, coba deh nonton video pembelajaran di YouTube atau platform belajar online. Biasanya penjelasannya lebih santai dan pakai gambar atau animasi, jadi lebih gampang dipahami. Diagram, grafik, dan ilustrasi juga bisa bantu kamu ngerti materi yang kelihatan rumit.
4. Aktif Berdiskusi dan Bertanya
Kalau nggak paham, jangan dipendem sendiri. Kamu bisa bertanya ke guru atau diskusi dengan teman. Kadang, penjelasan dari teman justru lebih mudah dipahami karena dijelaskan dengan gaya bahasa yang lebih mudah. Diskusi juga bikin belajar jadi nggak ngebosenin.
5. Buat Ringkasan dan Mind Map Sendiri
Terakhir, coba deh biasain bikin rangkuman menggunakan bahasamu sendiri. Nggak harus rapi kayak buku cetak, yang penting kamu mengerti. Kamu juga bisa pakai spidol/pulpen warna-warni, gambar, atau simbol biar lebih seru. Cara ini bantu banget buat nginget materi pas mau ulangan.
Baca Juga: 7 Solusi Belajar untuk Menghadapi Ulangan Matematika
Itulah rangkuman lengkap materi pelajaran Matematika kelas 10 untuk semester 1 dan semester 2 Kurikulum Merdeka. Mulai dari eksponen, barisan dan deret, vektor, trigonometri, sampai peluang, semua topik ini punya peran penting sebagai dasar buat materi di kelas 11 dan 12 nanti. Jadi, kalau kamu sudah paham dari sekarang, ke depannya bakal jauh lebih siap dan nggak gampang kaget sama materi yang makin menantang.
Dengan memahami semua topik ini secara bertahap, kamu nggak cuma lebih siap menghadapi ulangan dan ujian sekolah, tapi juga lebih percaya diri saat menghadapi ujian, seperti PTS, PAS, PAT, bahkan UTBK. Soal-soal yang awalnya kelihatan susah pun bisa terasa lebih masuk akal kalau kamu sudah ngerti konsep dasarnya.
Makanya, yuk mulai biasakan belajar dengan strategi yang tepat dan lakukan secara konsisten dari sekarang. Nggak perlu langsung jago, yang penting mau terus belajar dan berkembang sedikit demi sedikit. Biar makin semangat dan terbantu, kamu juga bisa belajar bareng ruangbelajar. Langsung aja download sekarang dan mulai perjalanan belajarmu menuju versi terbaik dari dirimu!
Referensi:
https://static.buku.kemdikbud.go.id/content/pdf/bukuteks/kurikulum21/Matematika-BS-KLS-X.pdf (Diakses pada 29 Januari 2026)
https://kuadran.co/blog/materi/materi-pelajaran-matematika-kelas-10-kurikulum-merdeka-semester-1-dan-2 (Diakses pada 29 Januari 2026)
https://kumparan.com/ragam-info/rangkuman-materi-matematika-kelas-10-kurikulum-merdeka-22dOkKEZg6p/full (Diakses pada 29 Januari 2026)